Construction of Subsets and set operations
A well-defined collection of distinct objects called elements or members.
Learning Outcomes:
- Write a set in its comprehensive form called set comprehension.
- Construct different subsets from a given set.
- Distinguish between closed interval and open interval.
- Demonstrate the ability to perform operations like union, intersection, set difference, and complement on sets using proper notation.
1️⃣ Set Comprehension: Writing Sets in Comprehensive Form
- Set comprehension is a way to define a set by describing the properties its members must satisfy instead of listing elements.
- Notation:
Reads as: “Set $ A $ is the set of all $ x $ such that $ x $ satisfies the property.”
- Example: Set of all even integers:

2️⃣ Constructing Subsets from a Given Set
- Given a set $ S = {a, b, c} $, subsets are any sets containing zero or more elements of $ S $.
- All subsets of $ S $:
- Visualized as a power set containing $2^n$ subsets for a set of $n$ elements.
- Diagram:

3️⃣ Distinguish Between Closed Interval and Open Interval
- Closed Interval $[a,b]$: Includes endpoints $a$ and $b$.
- Open Interval $(a,b)$: Excludes endpoints $a$ and $b$.
- Diagram:

🟢 Solid dots indicate inclusion (closed), hollow dots indicate exclusion (open).
4️⃣ Set Operations: Union, Intersection, Set Difference, Complement
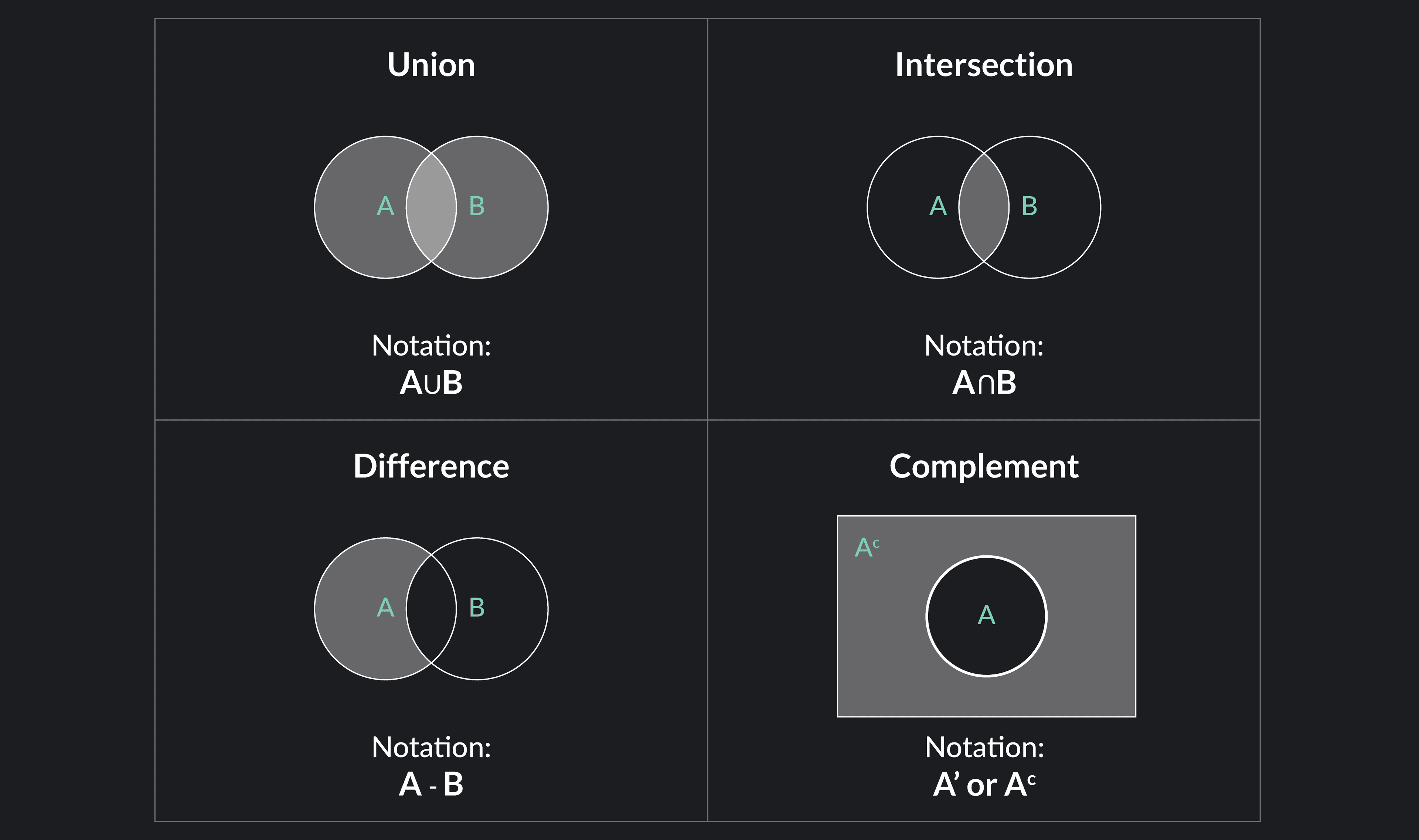
- Union ( $ A \cup B $ ): All elements in $ A $ or $ B $ or both. Example: $ A = {1,2}, B = {2,3} \Rightarrow A \cup B = {1,2,3} $
- Intersection ( $ A \cap B $ ): Elements common to both $ A $ and $ B $. Example: $ A \cap B = {2} $
- Set Difference ( $ A - B $ ): Elements in $ A $ but not in $ B $. Example: $ A - B = {1} $
- Complement ( $ A^c $ or $ \bar{A} $ ): Elements not in $ A $ relative to the universal set $ U $.
- Visual Diagram of Union and Intersection:

- Visual Diagram of Set Difference and Complement:


Exercise Questions 🤯





1) Which of the following is a correct representation of set comprehension?
A) $ {x \mid x \in \mathbb{N}, x is even} $ B) $ {x \in \mathbb{Z}, x is even} $ C) $ x is even, x \in \mathbb{N}, x } $ D) $ x is even, x \in \mathbb{Z}, x } $
Detailed Answer:
Proper set comprehension involves curly brackets and a “such that” ($\mid$ or “:”) description. A) is correct as it uses the proper notation:
$$ \{x \mid x \in \mathbb{N}, x \text{ is even}\} $$B is missing the surrounding curly brackets and “such that”. C and D are not valid set notations.
Correct Answer: A
2) Which of the following is the set of natural numbers that are multiples of 3 or 5?
A) $ {x \mid x \in \mathbb{N}, x \bmod 3 = 0 and x \bmod 5 = 0} $ B) $ {x \mid x \in \mathbb{N}, x \bmod 3 = 0 or x \bmod 5 = 0} $ C) $ {x \mid x \in \mathbb{N}, x \bmod 3 = 0 and x \bmod 5 = 0} $ D) $ {x \mid x \in \mathbb{N}, x \bmod 3 = 0 or x \bmod 5 = 0} $
Detailed Answer:
Multiples of 3 or 5 are numbers divisible by either 3 or 5. So, “or” is appropriate, not “and”. B) and D) are identical and correct.
Correct Answer: B or D
3) Which of the following sets represents students from Madras University who play both cricket and basketball?
Options: A) {Abbas, Akhil, Rakesh} B) {Bhuvan, Charan, Dayal, Kiran} C) {Kiran, Charan, Rakesh} D) {Aditya, Jaivardhan, Nithin, Rakesh}
Detailed Answer:
Find students in both the cricket and basketball sets.
- Basketball: {Abbas, Akhil, Aditya, Bhuvan, Charan, Dayal, Deepak, Kiran, Jaivardhan, Nithin, Rakesh}
- Cricket: {Kiran, Charan, Rakesh, Kiran, Chidambaram, Balachandra}
Intersection = {Kiran, Charan, Rakesh}
Correct Answer: C
4) What is the number of students who play all the three sports?
Options: 1 2 3 4
Detailed Answer:
Find students who are in the intersection of all three sets.
Volleyball: {Akhil, Charan, Deepak, Sunil, Karthik, Rakesh} Basketball: {Abbas, Akhil, Aditya, Bhuvan, Charan, Dayal, Deepak, Kiran, Jaivardhan, Nithin, Rakesh} Cricket: {Kiran, Charan, Rakesh, Kiran, Chidambaram, Balachandra}
Students present in all three: Check each name: Charan and Rakesh only.
So, number is 2.
Correct Answer: 2
5) Which of the following set represents the students from Madras University who play volleyball but not cricket?
Options: A) {Akhil, Rakesh, Sunil, Karthik} B) {Sunil, Karthik} C) {Deepak, Sunil, Bhuvan, Dayal, Nithin} D) {Abbas, Aditya, Bhuvan, Dayal, Kiran, Jaivardhan, Nithin}
Detailed Answer:
Volleyball: {Akhil, Charan, Deepak, Sunil, Karthik, Rakesh} Cricket: {Kiran, Charan, Rakesh, Kiran, Chidambaram, Balachandra}
Volleyball ∖ Cricket: Remove Charan and Rakesh from volleyball set. {Akhil, Deepak, Sunil, Karthik}
Correct Answer: A
6) Which of the following sets represent the students from Madras University who are not playing cricket?
Options: A) {Dayal, Deepak, Kiran, Jaivardhan} B) {Rakesh, Kiran, Chidambaram, Balachandra} C) {Bhuvan, Jaivardhan, Sunil, Chidambaram} D) {Sunil, Chidambaram, Karthik, Balachandra}
Detailed Answer:
Find students not in the cricket set.
Cricket: {Kiran, Charan, Rakesh, Kiran, Chidambaram, Balachandra}
Check who is not listed in this set. From the student list, the only correct option is D.
Correct Answer: D
7) If exams A and B are going to be conducted simultaneously, then what are the items that are required to be carried by the student to the exam centre?
Given sets: A: {Hall ticket, Pen, Calculator, Ruler, Pencil} B: {Compass, Pencil, Drafter, Ruler, Eraser, Sharpener, Hall ticket}
Options: A) {Hall ticket, Ruler, Pencil, Eraser, Sharpener, Pen, Drafter, Compass, Calculator} B) {Calculator, Ruler, Pencil, Hall ticket, Pen, Paper, Compass, Drafter} C) {Pen, Calculator, Pencil, Hall ticket, Ruler, Compass, Drafter, Eraser} D) {Ruler, Pencil, Compass, Drafter, Eraser, Sharpener, Hall ticket, Calculator}
Detailed Answer:
The student needs all items from both sets (union):
{Hall ticket, Pen, Calculator, Ruler, Pencil, Compass, Drafter, Eraser, Sharpener}
Option A covers all these exactly.
Correct Answer: A