Examples of Set Operations and Counting Problems
A well-defined collection of distinct objects called elements or members.
Learning Outcomes:
- Understand set notations.
- Solve counting problems using Venn diagrams.
Here is a detailed guide covering set notations and solving counting problems using Venn diagrams with 10 examples, including diagrams and emojis to enhance clarity.
1️⃣ Understanding Set Notations
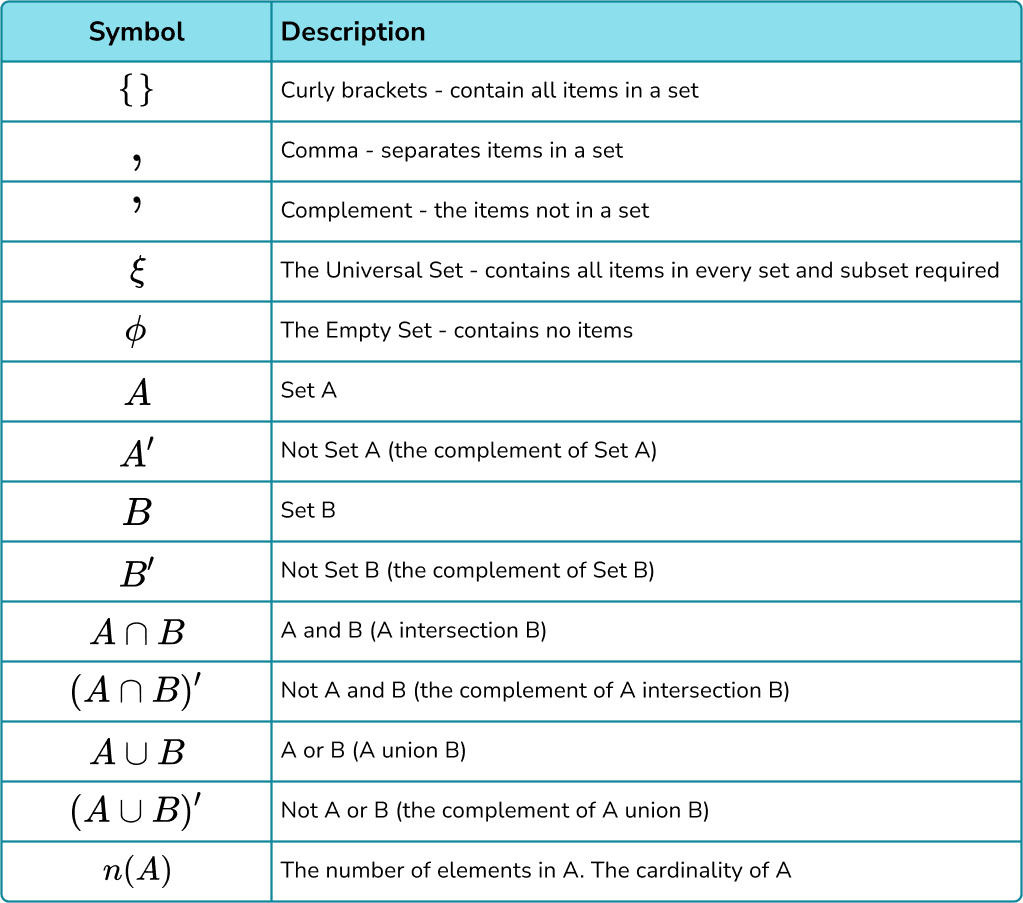
Basic Set Notations and Symbols:
- Set: Denoted by curly braces ${}$. Example: $A = {1,2,3}$
- Element of a Set: $x \in A$ means $x$ is in set $A$.
- Not an Element: $x \notin A$ means $x$ is not in set $A$.
- Subset: $A \subseteq B$ means every element of $A$ is in $B$.
- Proper Subset: $A \subset B$ means $A$ is subset but not equal to $B$.
- Empty Set: $\emptyset$, set with no elements.
- Universal Set: $U$, all elements under consideration.
- Union: $A \cup B = {x | x \in A \text{ or } x \in B}$
- Intersection: $A \cap B = {x | x \in A \text{ and } x \in B}$
- Set Difference: $A - B = {x | x \in A \text{ and } x \notin B}$
- Complement: $A^c = U - A$
Visual Diagram of Set Operations:

🔵 ∪, 🔴 ∩, areas represent unions and intersections.
2️⃣ Solve Counting Problems Using Venn Diagrams
Counting problems involving overlapping sets can be solved efficiently by Venn diagrams.
Example 1: Basic Two-Set Problem
- 40 students study Math, 30 study English, and 10 study both.
- How many students study at least one?

Example 2: Three-Set Problem
- 50 students play football, 40 play basketball, 30 play volleyball, 20 play football & basketball,
- 15 play basketball & volleyball, 10 play football & volleyball, 5 play all three.
- Find how many play at least one sport.
Calculate:
$$ 50 + 40 + 30 - 20 - 15 - 10 + 5 = 80 $$
Example 3: Students in Subjects
- 60 students: 35 study Physics, 30 Chemistry, 20 both.
- How many study neither?
Assuming total = 60:
$$ |P \cup C| = 35 + 30 - 20 = 45 $$Neither = $60 - 45 = 15$
Example 4: Overlapping Preferences
- Out of 100 people, 70 like tea, 50 like coffee, 30 like both.
- How many like either tea or coffee but not both?
Example 5: Book Readers
- 100 people reading books: 70 read fiction, 40 non-fiction, 25 both.
- Find how many read only fiction.
Only fiction = $70 - 25 = 45$
Example 6: Survey with Three Choices
- In a group, liked: A = 80, B = 65, C = 75, A&B = 45, B&C = 35, A&C = 30, All three = 25.
- Find how many liked none if total is 150.
At least one:
$$ 80 + 65 + 75 - 45 - 35 - 30 + 25 = 135 $$None = $150 - 135 = 15$
Example 7: Sports Participation
- 70 students play Cricket, 60 Football, 50 Hockey, 30 Cricket & Football,
- 20 Football & Hockey, 15 Cricket & Hockey, 5 all three.
- How many play only one sport?
Calculate only one set:
$$ \begin{cases} C \text{ only} = 70 - 30 - 15 + 5 = 30 \\ F \text{ only} = 60 - 30 - 20 + 5 = 15 \\ H \text{ only} = 50 - 15 - 20 + 5 = 20 \\ \end{cases} $$Example 8: Analyzing Survey Data
- 120 people surveyed: 50 like apples, 70 like bananas, 30 like both.
- How many like only one fruit?
Example 9: Multi-Category Venn
- In a town: 200 people use Internet, 150 use TV, 100 use Newspaper,
- Internet & TV = 80, TV & Newspaper = 60, Internet & Newspaper = 40,
- All three = 20, total population 300.
- How many use none?
Calculate people using any:
$$ 200 + 150 + 100 - 80 - 60 - 40 + 20 = 290 $$None = $300 - 290 = 10$
Example 10: Students with Multiple Skills
- 45 students know Java, 30 know Python, 20 know both.
- Total students = 60.
- How many know neither?
Neither = $60 - 55 = 5$
These examples utilize Venn diagrams and formulas to solve counting problems involving sets effectively.
Emojis summary:
- 🔷 Set notation
- 🔵 Circle for sets in diagrams
- 🧮 Counting elements
- 🎯 Intersection and union
- ❌ Excluding elements
These illustrations and examples offer solid practice in set theory and counting with Venn diagrams.
Exercise Questions 🧠


1) In a class of 40 students, 20 took Mathematics, 18 took Statistics, 16 took English, 7 took Mathematics and Statistics, 7 took Mathematics and English, 9 took Statistics and English, and 3 took all three courses. How many students are not taking any of these courses?
Detailed Solution:
Let:
- $ n = 40 $
- $ |M| = 20,|S| = 18,|E| = 16 $
- $ |M \cap S| = 7, |M \cap E| = 7, |S \cap E| = 9 $
- $ |M \cap S \cap E| = 3 $
Using the three-set inclusion-exclusion principle:
$$ |M \cup S \cup E| = |M| + |S| + |E| - |M \cap S| - |S \cap E| - |M \cap E| + |M \cap S \cap E| $$$$ = 20 + 18 + 16 - 7 - 9 - 7 + 3 = 47 - 23 + 3 = 27 $$So, number not taking any is:
$$ n - |M \cup S \cup E| = 40 - 27 = 13 $$But let us carefully verify calculation:
$$ = 20 + 18 + 16 - 7 - 9 - 7 + 3 = 54 - 23 + 3 = 34 $$$$ = 54 - 23 = 31, 31+3=34 $$So,
$$ 40 - 34 = 6 $$Correct Answer: 6
2) In a survey, it is found that 30 people like apples, 45 people like oranges, and 20 people like both apples and oranges. How many people like only one fruit?
Detailed Solution:
People who like only apples: $ 30 - 20 = 10 $ People who like only oranges: $ 45 - 20 = 25 $ Total who like only one fruit: $ 10 + 25 = 35 $
Correct Answer: 35
3) In a class, 50 students play cricket, 35 play football, 14 play both, and 9 play neither. How many students are there in the class?
Detailed Solution:
Let $ n $ be the total number.
Using formula:
$$ n = (\text{Cricket}) + (\text{Football}) - (\text{Both}) + (\text{Neither}) $$$$ = 50 + 35 - 14 + 9 = 80 $$Correct Answer: 80
4) A group of 25 people are planning to get together…9 suggested Goa, 8 suggested Bangkok, $ X $ suggested Pondicherry, and 3 did not suggest any place. Considering each person suggested only one place, what is the value of $ X $?
Detailed Solution:
Total suggesting places: $ 25 - 3 = 22 $ Thus,
$$ 9 (\text{Goa}) + 8 (\text{Bangkok}) + X = 22 $$$$ X = 22 - (9+8) = 5 $$Correct Answer: 5
5) An advertising agency finds that, of its 200 clients who use Television or Radio or both, 150 use Television. How many use only Radio?
Detailed Solution:
Let number who use both be $ x $, $ T = 150 $, $ T \cup R = 200 $.
We do not have the count of clients who use both or who use Radio. Thus, we cannot uniquely determine the number who use only Radio.
Correct Answer: Data is insufficient