Functions

A well-defined collection of distinct objects called elements or members.

1️⃣ Define Function, Domain, Co-domain, and Range

• Function: A relation $f$ from set $A$ (domain) to set $B$ (co-domain) that assigns each element in $A$ exactly one element in $B$. Denoted as $f: A \to B$.
• Domain ($A$): The set of input values over which the function is defined. Example: $A = {1,2,3}$.
• Co-domain ($B$): The set where outputs of the function lie. Example: $B = {a,b,c,d}$.
• Range: The subset of the co-domain actually mapped by the function. For example, if $f(1) = a, f(2) = b, f(3) = a$, then range $= {a,b}$.

Diagram: Function Mapping

🎯 Each arrow shows the mapping from domain to co-domain. Each domain element maps to exactly one codomain element.

2️⃣ Identify Domain and Range of a Given Function

• Example: $f:\mathbb{R} \to \mathbb{R}$, defined by $f(x) = x^2$.
• Domain: All real numbers ($\mathbb{R}$).
• Range: Non-negative real numbers $[0, \infty)$, because squaring any real number can’t be negative.

Diagram of Domain to Range

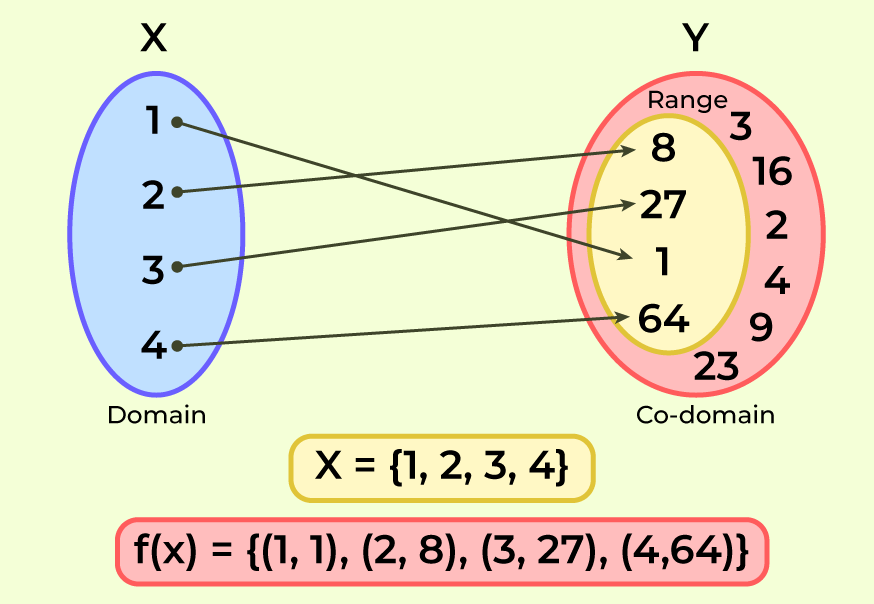
🟢 All inputs from domain map to outputs in range.

3️⃣ Classify a Function: Injective, Surjective, Both or Neither

• Injective (One-to-One): Different inputs map to different outputs.
  • Example: $f(x) = 2x$ over real numbers (distinct inputs produce distinct outputs).
• Surjective (Onto): Every element in the co-domain is mapped to by some input.
  • Example: $f(x) = x^3$ over real numbers (every real number has a cube root).
• Bijective: Both injective and surjective.
• Neither: Does not satisfy injective or surjective properties.

Diagram Examples

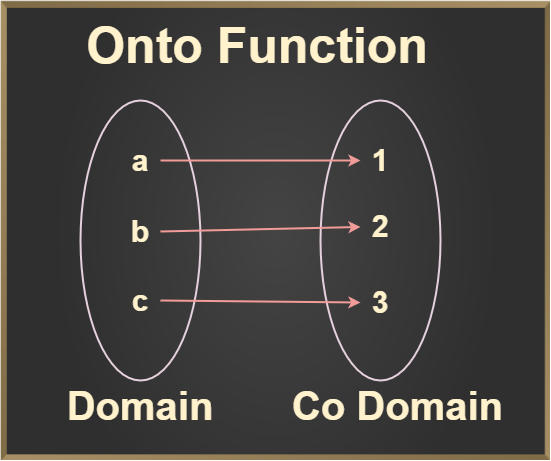
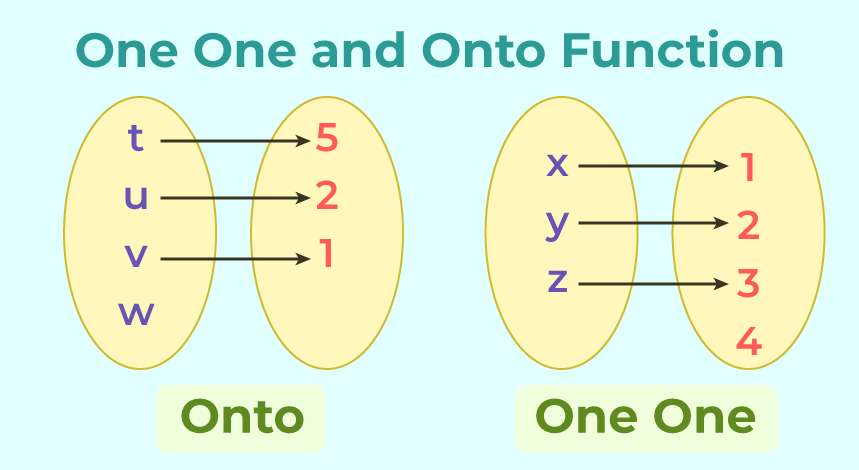
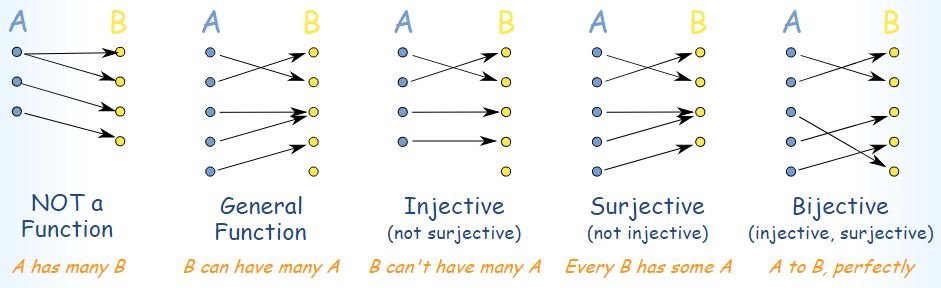
🔄 Injection: no two arrows go to the same place. Finish of the co-domain: surjection. Both: bijection.

4️⃣ Define Bijection

• Bijection: A function that is both injective and surjective. It has an inverse function $f^{-1}$ that maps the co-domain back to domain one-to-one.
• Example: $f:\mathbb{R} \to \mathbb{R}$, $f(x) = x + 3$
• Inverse is $f^{-1}(y) = y - 3$.
• Properties: Bijections pair elements perfectly without overlaps or gaps.

Diagram of Bijection and Inverse

🎯 Each input maps uniquely to an output and vice versa.

Summary Emojis

• 🎯 Function mapping
• 🔢 Inputs and outputs
• 🔄 Injection, surjection visuals
• 🚀 Bijection and inverse

This detailed guide provides a clear understanding of functions and their classification, accompanied by rich visuals.

1. Define a function, domain, co-domain, and range of a function.

• Function: A relation from set $A$ (domain) to set $B$ (co-domain) where every element of $A$ maps to exactly one element of $B$. Notation: $f: A \to B$.
• Domain: The set of all possible inputs, $A$.
• Co-domain: The set in which outputs lie, $B$.
• Range: The set of all actual outputs $f(x)$ for $x \in A$, subset of $B$.

Example: $f(x) = x^2$, $A = \mathbb{R}$, $B = \mathbb{R}$, range = $[0, \infty)$.

🎯

2. Identify the domain and range of a given function

Given $f(x) = x^2$:

• Domain = All real numbers $\mathbb{R}$.
• Range = All non-negative real numbers $[0, \infty)$ since squares are $\geq 0$.

🟢

3. Classify a function as injective, surjective, both, or neither

• Injective (One-to-one): No two different inputs share the same output. Example: $f(x) = 2x$ over $\mathbb{R}$ (each input maps to distinct outputs).
• Surjective (Onto): Every element in co-domain is covered by some input. Example: $f(x) = x^3$ over $\mathbb{R}$.
• Bijective: Both injective and surjective; one-to-one and onto.

🔄

4. Define bijection with examples

• Bijection: A function that is both injective and surjective. It has an inverse function.

Example: $f: \mathbb{R} \to \mathbb{R}, f(x) = x + 3$. Inverse is $f^{-1}(y) = y - 3$.

🚀

Exercise Questions 🤯