Natural Numbers and their operations
Of course! Let’s dive deep into the world of Natural Numbers and their operations. We’ll start from the very basics and build up to the properties that govern them.
Identifying Natural Numbers and Integers
Natural numbers are positive whole numbers, used for counting: 1, 2, 3, 4, 5, ….12 Integers include all positive and negative whole numbers and zero: …, -3, -2, -1, 0, 1, 2, 3, ….3
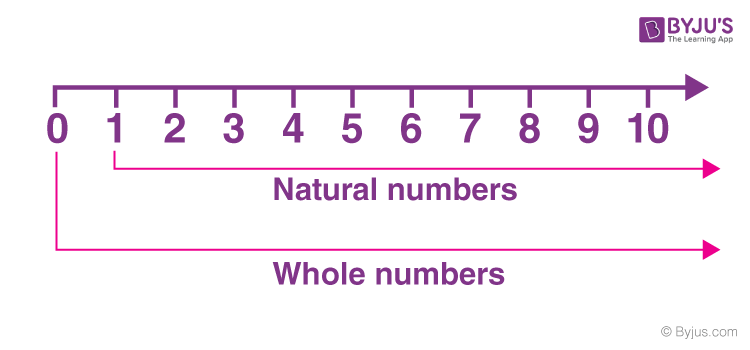
- Example images: Diagrams often show natural numbers on a number line starting at 1, with integers extending in both directions to negative numbers.41 4
- Natural numbers set: $\mathbb{N} = {1, 2, 3, 4, 5, \dots}$.21
- Integers set: $\mathbb{Z} = {\dots, -2, -1, 0, 1, 2, \dots}$.53
Distinguishing Between Notations: ($\mathbb{N}$), ($\mathbb{Z}$), ($\mathbb{Z}_n$)
- N ($\mathbb{N}$): Natural numbers set ($1, 2, 3, …$).[^6]1
- Z ($\mathbb{Z}$): Integers set ($…, -2, -1, 0, 1, 2, …$).[^6]
- ZN ($\mathbb{Z}_n$): Modular integers—the set of possible remainders when dividing by $n$ ($0,1,\ldots, n-1$).

Example: Venn diagram notation can show relationships; N could fit inside Z on a diagram.[^7][^6] 4
Multiplication and Division as Addition/Subtraction
- Multiplication is repeated addition:
Imagine four groups, each with three objects—adding up all objects gives the same as multiplication.[^8]
- Division is repeated subtraction:
The number of times 5 is subtracted until reaching zero is the quotient (here, 3).[^9][^8]
Visual: Diagrams often show sets of objects grouped or repeatedly removed, or jumps on a number line illustrating subtraction. 4
Quotient, Remainder, and Modulus
- Quotient: The result of division (number of times divisor “fits” in dividend).
- Remainder: What’s left after dividing as far as possible.
- Modulus (mod): The remainder after division.
Example: $14 \div 5 = 2$ remainder $4$, so $14$ mod $5 = 4$.
Visual: Number lines or division diagrams often show repeated subtraction steps, grouping leftover items as remainder.[^9]
Factors and Prime Factorization
- Factors: Numbers that divide another exactly. Example: 12’s factors are 1, 2, 3, 4, 6, 12.
- Prime Factorization: Breaking a number into prime numbers multiplied together. Example: 12 = 2 × 2 × 3 = $2^2 \times 3$.
Visual: Factor trees are diagrams showing branches, each end-point is a prime number.1 4
Table: Sets and Concepts
| Concept | Notation | Example | Image Reference |
|---|---|---|---|
| Natural numbers | $\mathbb{N}$ | 1,2,3,… | 4 |
| Integers | $\mathbb{Z}$ | …, -1,0,1 | 5 |
| Modular integers | $\mathbb{Z}_n$ | 0,1,…,n-1 | 4 |
| Factors of 12 | n/a | 1,2,3,4,6,12 | 4 |
| Prime factorization | n/a | 12 = $2^2\times3$ | 4 |
Exercise Questions 🤯


1) How many natural numbers are there in the given list?
List: 22, -17, 47, -2000, 0, 1, 43, 1729, 6174, -63, 100, 32, -9.
Solution: Natural numbers ($\mathbb{N}$) are positive whole numbers: ${1, 2, 3, …}$, and do not include 0 or negatives.[^1][^2] Filtering the list:
- 22 — Yes
- -17 — No
- 47 — Yes
- -2000 — No
- 0 — No
- 1 — Yes
- 43 — Yes
- 1729 — Yes
- 6174 — Yes
- -63 — No
- 100 — Yes
- 32 — Yes
- -9 — No
There are 8 natural numbers: 22, 47, 1, 43, 1729, 6174, 100, 32.[^2] [^3]
2) If we distribute 3 pens to each student and 4 pens remain, what is the value of M?
Solution: Given: Total pens = 70, pens per student = 3, pens left over = 4, number of students = $M$.
Use Division Algorithm:
$$ \text{Total} = (\text{Pens per student} \times M) + \text{Remainder} $$So:
$$ 70 = (3 \times M) + 4 \implies 66 = 3M \implies M = \frac{66}{3} = 22 $$Thus, M = 22.[^4]
4) If z mod 31 and z mod 74. Which of the following is (are) possible values for z?
Solution: Possible remainders from modulus operations must be between 0 and one less than the divisor:[^4]
- For $z \mod 31$: remainder must be in $$
- For $z \mod 74$: remainder must be in $$
Test options:
- $z = 25$: Valid for both
- $z = 34$: Invalid for mod 31
- $z = 58$: Invalid for mod 31
- $z = 67$: Invalid for mod 31
Thus, 25 is the only possible value.
5) If Sheetal’s birthday is on the Pth of October and Karthik’s is on the Qth of November… find the value of P + 20.
Solution: P and Q are perfect squares, October/November birthdays, and Sheetal is 10 days before Karthik:
Perfect squares up to 31: 1, 4, 9, 16, 25 Let $P = 25$ (25th October).
If Karthik is born 10 days later: Days left in October after 25th = 31-25 = 6; Karthik’s birthday is 4th November, which is also a perfect square.
Thus: P = 25, Q = 4 $P + 20 = 25 + 20 = 45$