Real and Complex Numbers
Real Numbers (R) include all rational numbers plus all irrational numbers (numbers that cannot be expressed as fractions). This makes the real numbers a complete set covering every possible point on the number line.
Learning Outcomes:
- Know how rational numbers extend to real numbers.
- Identify irrational numbers and complex numbers.
- Classify a real number as an integer, rational, or irrational number.
1️⃣ How Rational Numbers Extend to Real Numbers
- Rational Numbers ($\mathbb{Q}$) are numbers expressed as fractions $\frac{p}{q}$, where $p, q$ are integers, $q \neq 0$. Examples: $\frac{1}{2}, 0.75, -3$.12
- Real Numbers ($\mathbb{R}$) include all rational numbers plus all irrational numbers (numbers that cannot be expressed as fractions). This makes the real numbers a complete set covering every possible point on the number line.3
- Diagram:
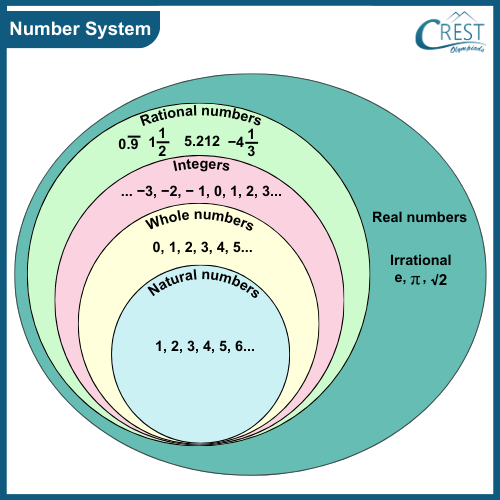
📏 Visualization: Real numbers include both rational and irrational, filling the number line without gaps.
2️⃣ Identify Irrational Numbers and Complex Numbers
- Irrational Numbers are real numbers that cannot be written as a simple fraction $\frac{p}{q}$. Their decimals are non-terminating and non-repeating. Examples: $\pi$, $\sqrt{2}$, $e$.4
- Complex Numbers combine real and imaginary parts, written as $a + bi$, where $i = \sqrt{-1}$.56 Example: $3 + 4i$, where 3 is the real part and 4i is the imaginary part.
- Diagram for Complex Numbers:
🎯 Complex numbers plotted on a plane: horizontal axis is real part, vertical axis is imaginary part.
3️⃣ Classify a Real Number as Integer, Rational, or Irrational
- Classification:
| Number Type | Description | Examples |
|---|---|---|
| Integer ($\mathbb{Z}$) | Whole numbers including negatives, zero, positives | $-3, 0, 7$ |
| Rational ($\mathbb{Q}$) | Can be written as fraction $\frac{p}{q}$ | $\frac{1}{2}, -4, 0.75$ |
| Irrational | Cannot be expressed as fraction; decimals non-terminating/non-repeating | $\pi, \sqrt{2}$ |
- Venn diagram of number sets:
🔢 All integers are rational, all rationals and irrationals together form real numbers.
Emojis highlight key ideas:
- 📏 Number lines
- 🎯 Complex plane
- 🔢 Classification
Exercise Questions 🤯


1) Which of the following statement(s) is(are) false?
- The sum of two natural numbers is always a natural number.
- The difference between two integers is always an integer.
- The product of two rational numbers is always a real number.
- The product of two irrational numbers is always an irrational number.
Detailed Answer:
- The sum of two natural numbers is always a natural number: True. Example: $ 7 + 5 = 12 $ (still a natural number).
- The difference between two integers is always an integer: True. Example: $ -3 - 7 = -10 $ (still an integer).
- The product of two rational numbers is always a real number: True. All rational numbers are real numbers, so their product is always a real number.
- The product of two irrational numbers is always an irrational number: False! Example: $ \sqrt{2} \times \sqrt{2} = 2 $ (which is rational). Sometimes the product can be rational.
Correct Answer: The fourth statement is false: The product of two irrational numbers is always an irrational number.
2) How many irrational numbers are there in the given list?
Given list: $\sqrt{3},\ 2.5, \sqrt{49},\ \frac{17}{2},\ 22, \pi, -35, \sqrt{6}, 1729, -20000$
Detailed Answer:
Irrational numbers are real numbers that cannot be expressed as a simple fraction.
- $\sqrt{3}$: Irrational (not a perfect square, non-repeating, non-terminating decimal)
- $2.5$: Rational ($5/2$)
- $\sqrt{49}$: $= 7$, rational
- $\frac{17}{2}$: Rational
- $22$: Rational
- $\pi$: Irrational (never-ending, non-repeating decimal)
- $-35$: Rational (integer)
- $\sqrt{6}$: Irrational (not a perfect square)
- $1729$: Rational (integer)
- $-20000$: Rational (integer)
So, the irrational numbers are: $\sqrt{3}, \pi, \sqrt{6}$
Count: 3
Correct Answer: 3 irrational numbers in the list.
3) How many integers are there in the given list?
Given list: $\sqrt{3},\ 2.5, \sqrt{49},\ \frac{17}{2},\ 22, \pi, -35, \sqrt{6}, 1729, -20000$
Detailed Answer:
Integers are whole numbers, positive, negative, or zero (without fractional/decimal part):
- $\sqrt{3}$: Not an integer.
- $2.5$: Not an integer.
- $\sqrt{49} = 7$: Integer.
- $\frac{17}{2}=8.5$: Not an integer.
- $22$: Integer.
- $\pi$: Not an integer.
- $-35$: Integer.
- $\sqrt{6}$: Not an integer.
- $1729$: Integer.
- $-20000$: Integer.
So, the integers are: $\sqrt{49} (=7),\ 22,\ -35,\ 1729,\ -20000$
Count: 5
Correct Answer: 5 integers in the list.
4) Which of the following statement(s) is(are) true?
- $ \sqrt{2} $ is a complex number.
- Real numbers extend rational numbers.
- None of these.
Detailed Answer:
- $ \sqrt{2} $ is a real and irrational number, which is also technically a special case of a complex number (since all real numbers are complex of the form $a + 0i$), but usually when we say “complex number,” we refer to numbers with a nonzero imaginary part.
- Real numbers extend (include) all rational numbers, so this is true (every rational is real, but not every real is rational).
- “None of these” is incorrect because one correct statement is present.
Correct Answer: Real numbers extend rational numbers.
5) Which of the following rational numbers are greater than $ \sqrt{2} $ and less than $ \sqrt{3} $?
Options:
- $ \frac{9}{5} $
- $ \frac{3}{2} $
- $ \frac{5}{3} $
- $ \frac{17}{10} $
Detailed Answer:
First, find decimal values for comparison:
- $ \sqrt{2} \approx 1.414 $
- $ \sqrt{3} \approx 1.732 $
Convert each option to decimal:
- $ \frac{9}{5} = 1.8 $
- $ \frac{3}{2} = 1.5 $
- $ \frac{5}{3} \approx 1.6667 $
- $ \frac{17}{10} = 1.7 $
Now, select values $ x $ such that $ \sqrt{2} < x < \sqrt{3} $ (i.e., $ 1.414 < x < 1.732 $):
- $ \frac{9}{5} = 1.8 $: Not in the range.
- $ \frac{3}{2} = 1.5 $: In the range.
- $ \frac{5}{3} \approx 1.6667 $: In the range.
- $ \frac{17}{10} = 1.7 $: In the range.
Correct answers: $ \frac{3}{2}, \frac{5}{3}, \frac{17}{10} $ are greater than $ \sqrt{2} $ and less than $ \sqrt{3} $.
