Relations
A well-defined collection of distinct objects called elements or members.
1️⃣ Compute the Cartesian Product of Two Non-Empty Sets
- Definition: The Cartesian Product $ A \times B $ of sets $ A $ and $ B $ is the set of all ordered pairs $(a, b)$ such that $a \in A$ and $b \in B$.
- Example: $ A = {1, 2}, B = {x, y} $ Then:
Diagram: Cartesian Product
🔢 Each point represents an ordered pair from the sets.
2️⃣ Identify Relations as a Subset of the Cartesian Product
- A Relation $ R $ from set $ A $ to $ B $ is a subset of the Cartesian product $ A \times B $.
- Each related pair $ (a, b) \in R $.
- Example: $ A = {1,2}, B = {x,y} $ Relation $ R = { (1,x), (2,y) } \subseteq A \times B $.
- Relations express connections or associations between elements of $ A $ and $ B $.
Diagram: Relation as a subset
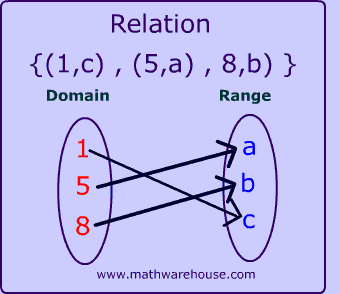
🔗 Arrows show pairs included in the relation.
3️⃣ Properties of Relations: Reflexive, Symmetric, Transitive, Antisymmetric
- Reflexive: For every $a \in A$, $(a, a) \in R$. Example: Equality relation.
- Symmetric: If $(a, b) \in R$, then $(b, a) \in R$. Example: “Is sibling of” relation.
- Transitive: If $(a, b) \in R$ and $(b, c) \in R$, then $(a, c) \in R$. Example: “Is ancestor of” relation.
- Antisymmetric: If $(a, b) \in R$ and $(b, a) \in R$, then $a = b$. Example: “Less than or equal to” ($\leq$).
Diagram: Properties Representation
Examples for each:
| Property | Example Relation | Explanation |
|---|---|---|
| Reflexive | Equality $=$ | Every element equal to itself |
| Symmetric | Friendship | If A is friend of B, B is friend of A |
| Transitive | “Ancestor of” | If A is ancestor of B and B of C, then A of C |
| Antisymmetric | ≤ relation on numbers | If $a ≤ b$ and $b ≤ a$, then $a = b$ |
4️⃣ Define Equivalence Relation and Equivalence Classes
- Equivalence Relation: A relation $R$ on a set $A$ that is reflexive, symmetric, and transitive.
- Equivalence Class: For $a \in A$, the equivalence class $[a]$ is:
All elements related to $a$ form the class.
Examples of Equivalence Relations:
- Equality ($=$): every element equal to itself satisfies all properties.
- Congruence modulo $n$:
- Similarity of triangles: Two triangles are related if they are similar.
- Parallelism of lines: Lines related if parallel.
- Same birthdate: People with same birthdate are related.
Diagram: Equivalence Classes Partitioning a Set
Partitioned subsets represent equivalence classes, covering entire set without overlap.
Summary Emojis:
- 🔢 Cartesian product pairs
- 🔗 Relation arrows
- ✅ Properties ✔️
- 🎯 Equivalence classes partition
This detailed explanation with illustrations builds a solid conceptual foundation for understanding relations in sets.Here is a detailed guide explaining Cartesian products, relations, their properties, and equivalence relations with examples, diagrams, and emojis to enhance understanding.
Exercise Questions 🐻❄️
1) Let $A = {1,4}$ and $B = {2,4,6,8}$. Which of the following is the Cartesian product of $A$ and $B$?
Detailed Answer:
By definition,
$$ A \times B = \{(a, b)\ |\ a \in A, b \in B\} $$So:
- $(1,2), (1,4), (1,6), (1,8), (4,2), (4,4), (4,6), (4,8)$
Correct Option: ${(1,2), (1,4), (1,6), (1,8), (4,2), (4,4), (4,6), (4,8)}$
3) Suppose the Cartesian product $A \times B$ has 18 elements. Which of the following options may represent the number of elements in $A$ and $B$?
Detailed Answer:
If $|A| \times |B| = 18$. Possible factorizations:
- $ 3 \times 6 = 18 $
- $ 6 \times 3 = 18 $
- $ 2 \times 9 = 18 $
- $ 9 \times 2 = 18 $
All these pairs are present in options.
Correct Answer: All valid pairs:
- 3, 9
- 2, 9
- 9, 9 (Incorrect because 9 × 9 = 81, not 18)
- 6, 3
So, A, B, D.
4) Which of the following statement(s) is(are) true?
- In a set, order of elements is not important.
- A relation is a subset of Cartesian product.
- In each pair of Cartesian product, order is not important.
- All of the above
Detailed Answer:
- Order in a set is not important: True
- A relation is a subset of a Cartesian product: True
- In each pair of Cartesian product, order is important (so option 3 is false).
- Therefore, “All of the above” is not true.
Correct Answer: The first two statements only.
5) Let $B = {\text{Anil}, \text{Ramu}, \text{Suraj}}$ and $G = {\text{Neha}, \text{Keerthi}}$ be the sets of boys and girls, respectively. Ramu is brother of Neha, Anil is brother of Keerthi, Suraj is brother of Neha and Keerthi. Relation $R$ is: $ R = {(a, b) \mid (a, b) \in B \times G, a is brother of b} $.
Detailed Answer:
Map brothers to girls:
- Ramu is brother of Neha: (Ramu, Neha)
- Anil is brother of Keerthi: (Anil, Keerthi)
- Suraj is brother of Neha and Keerthi: (Suraj, Neha), (Suraj, Keerthi)
So $R$ = {(Anil, Keerthi), (Ramu, Neha), (Suraj, Neha), (Suraj, Keerthi)}
Correct Option: ${(Anil, Keerthi), (Ramu, Neha), (Suraj, Neha), (Suraj, Keerthi)}$
6) Let $S$ be a set of students who are studying B.Tech first year at I.I.T Madras. Which of the following relations is a symmetric relation?
Detailed Answer:
- “Younger than” or “got more marks”: Not symmetric.
- “Classmate of”: If $a$ is classmate of $b$, $b$ is classmate of $a$ (symmetric).
- “Taller than”: Not symmetric.
Correct Answer: ${(a, b) \mid a, b \in S, a \text{ is classmate of } b}$
7) Which of the following statement(s) is(are) incorrect?
- An equivalence relation partitions a set.
- An equivalence class is same as equivalence relation.
- Antisymmetric relation is an equivalence relation.
- Elements in Cartesian product will only be in pairs.
Detailed Answer:
- An equivalence relation partitions a set: True
- Equivalence class is not the same as equivalence relation: Incorrect
- Antisymmetric relation is not an equivalence relation: Incorrect
- Elements in Cartesian product are always ordered pairs: True
Correct Answers:
- “An equivalence class is same as equivalence relation.”
- “Antisymmetric relation is an equivalence relation.”
⁂