Rectangular Coordinate system
A well-defined collection of distinct objects called elements or members.
Learning Outcomes
- Know the basics of the rectangular coordinate system and the quadrants.
- Recognize, show, or plot a point on the coordinate plane.
1️⃣ Basics of the Rectangular Coordinate System and Quadrants
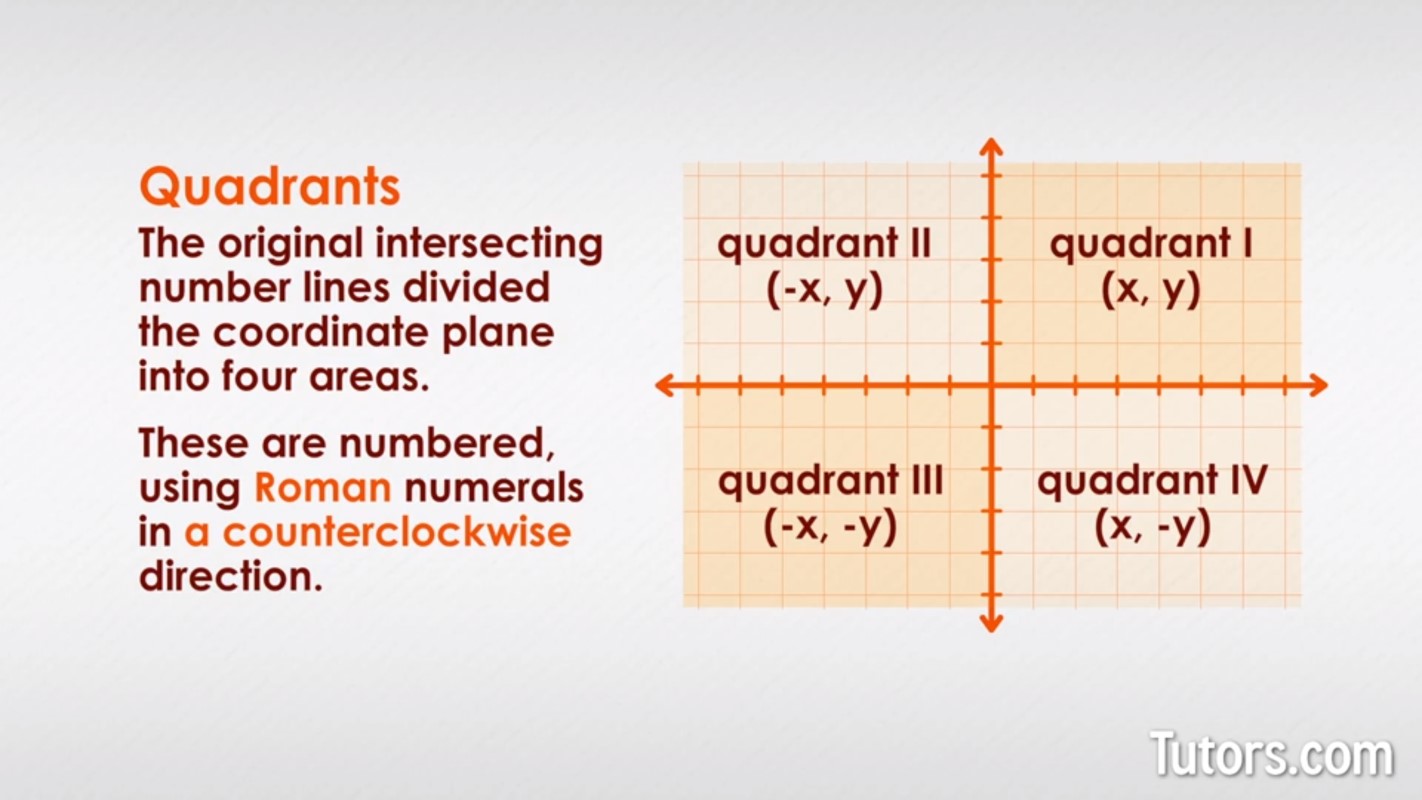
The rectangular coordinate system (also called the Cartesian coordinate system) uses two number lines that intersect at right angles at a point called the origin (0,0).
- The horizontal axis is the $ x $-axis.
- The vertical axis is the $ y $-axis.
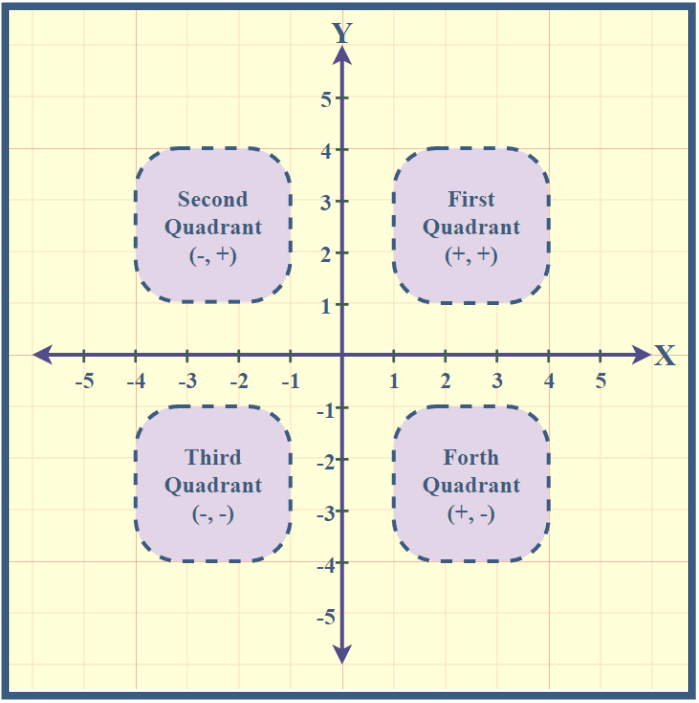
These axes divide the plane into four quadrants, numbered counterclockwise as follows:
- Quadrant I: $ x > 0, y > 0 $ (top right)
- Quadrant II: $ x < 0, y > 0 $ (top left)
- Quadrant III: $ x < 0, y < 0 $ (bottom left)
- Quadrant IV: $ x > 0, y < 0 $ (bottom right)
Coordinate Plane Image

- The axes meet at the origin $(0,0)$, and each point in the plane is represented as an ordered pair $(x, y)$.12
2️⃣ Recognize, Show, or Plot a Point on the Coordinate Plane
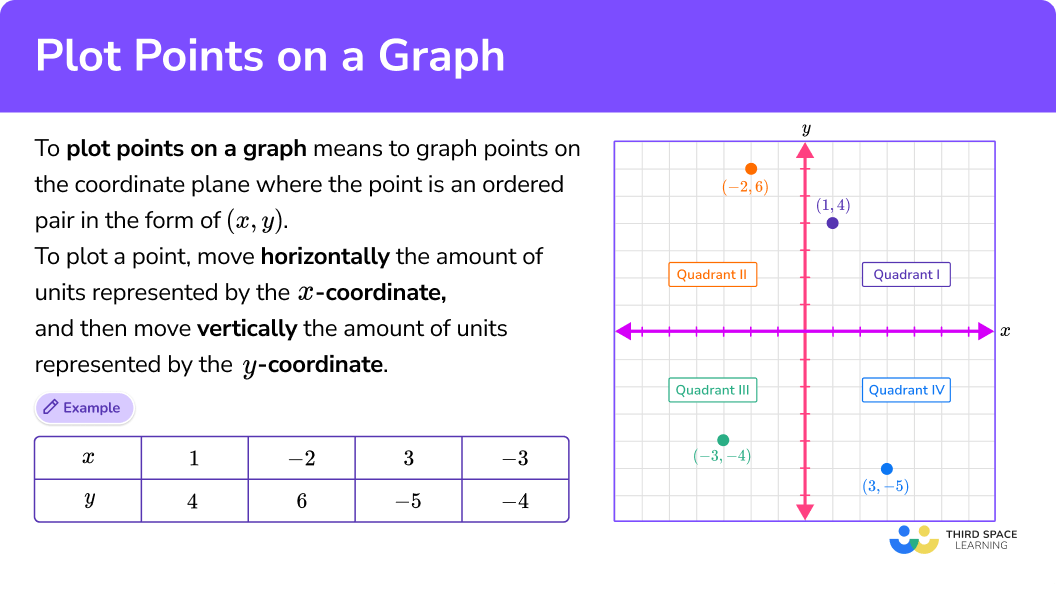
To plot a point such as $ (3, -2) $:
- Start at the origin $(0,0)$.
- Move 3 units right along the $ x $-axis (since $ x = +3 $).
- Move 2 units down along the $ y $-axis (since $ y = -2 $).
- Mark the point here.
General Rule:
- The first value in $(x, y)$ is the horizontal movement (right if positive, left if negative).
- The second value is the vertical movement (up if positive, down if negative).
Diagram: Plotting Points
Examples:
- Point $ (4, 5) $ lies in Quadrant I (both positive).
- Point $ (-3, 2) $ lies in Quadrant II (negative $ x $, positive $ y $).
- Point $ (-2, -4) $ lies in Quadrant III (both negative).
- Point $ (6, -7) $ lies in Quadrant IV (positive $ x $, negative $ y $).
For more details and illustrations, see:
Exercise Questions 🤯

Hello! On this Wednesday evening here in India, I would be happy to help you with these questions on the rectangular coordinate system. Let’s break them down one by one.
Question 1: Locating Points
The Question: Choose the correct option with respect to the points $P(5, -3)$, $Q(-3, 3)$, $R(0, -100)$, and $S(-2.5, 0)$ on the rectangular coordinate system.
- Point R does not lie in any quadrant
- Points P and R lie in Quadrant III
- Points S and Q lie in Quadrant II
- Points R and S cannot be represented on the rectangular coordinate system
Core Concepts: Quadrants and Axes
To solve this, we need to know where points are located based on the signs of their x and y coordinates.
- Quadrant I: x is positive (+), y is positive (+)
- Quadrant II: x is negative (-), y is positive (+)
- Quadrant III: x is negative (-), y is negative (-)
- Quadrant IV: x is positive (+), y is negative (-)
- On an Axis: If either the x or y coordinate is 0, the point is not in a quadrant but lies on one of the axes.
- If x = 0, the point is on the y-axis.
- If y = 0, the point is on the x-axis.
Detailed Solution:
Let’s analyze the location of each point:
- P(5, -3): The x-coordinate (5) is positive, and the y-coordinate (-3) is negative. A (+, -) point lies in Quadrant IV.
- Q(-3, 3): The x-coordinate (-3) is negative, and the y-coordinate (3) is positive. A (-, +) point lies in Quadrant II.
- R(0, -100): The x-coordinate is 0. This means the point lies directly on the y-axis. Points on an axis are not in any quadrant.
- S(-2.5, 0): The y-coordinate is 0. This means the point lies directly on the x-axis. Points on an axis are not in any quadrant.
Now let’s evaluate the given options:
- Point R does not lie in any quadrant: This is TRUE. As we determined, R(0, -100) lies on the y-axis.
- Points P and R lie in Quadrant III: This is FALSE. P is in Quadrant IV, and R is on the y-axis.
- Points S and Q lie in Quadrant II: This is FALSE. Q is in Quadrant II, but S is on the x-axis.
- Points R and S cannot be represented on the rectangular coordinate system: This is FALSE. Any ordered pair of real numbers, including those with zero, can be precisely located on the plane.
Final Answer: The only correct option is “Point R does not lie in any quadrant”.
Question 2: Fundamentals of the Coordinate System
The Question: Which of the following is/are correct with respect to the rectangular coordinate system? (Multiple Select Question)
- The horizontal line is called Y-axis
- The point of intersection of the X and Y axes is called the origin
- The vertical line is called X-axis
- Any point on the coordinate plane can be represented as an ordered pair (x, y)
Core Concepts: Definitions
- x-axis: The horizontal number line that passes through the origin.
- y-axis: The vertical number line that passes through the origin.
- Origin: The specific point $(0, 0)$ where the x-axis and y-axis intersect.
- Ordered Pair: The standard notation $(x, y)$ that gives the unique “address” of any point by specifying its horizontal distance (x) and vertical distance (y) from the origin.
Detailed Solution:
Let’s check each statement against the definitions:
- The horizontal line is called Y-axis: This is FALSE. The horizontal line is the x-axis.
- The point of intersection of the X and Y axes is called the origin: This is TRUE. This is the definition of the origin.
- The vertical line is called X-axis: This is FALSE. The vertical line is the y-axis.
- Any point on the coordinate plane can be represented as an ordered pair (x, y): This is TRUE. This is the fundamental purpose of the coordinate system.
Final Answer: The two correct statements are “The point of intersection of the X and Y axes is called the origin” and “Any point on the coordinate plane can be represented as an ordered pair (x, y)”.
Question 3: Identifying Incorrect Representations
The Question: Identify the incorrect options for the representation of a point on the coordinate plane. (Multiple Select Question)
Core Concepts: Coordinate Conventions
This question tests the same concepts as Question 1 but asks you to find the mistakes. Let’s list the correct conventions first:
- Quadrant I: (+, +)
- Quadrant II: (-, +)
- Quadrant III: (-, -)
- Quadrant IV: (+, -)
- On X-axis: (x, 0) or (±, 0)
- On Y-axis: (0, y) or (0, ±)
- Origin: (0, 0)
Detailed Solution:
Now we will evaluate each option to see if it’s correct or incorrect. The goal is to identify the incorrect ones.
- Quadrant I : (+, +): This statement is CORRECT.
- Quadrant IV : (-, -): This statement is INCORRECT. Quadrant IV points have a positive x and a negative y, so the form is (+, -).
- Quadrant II : (-, -): This statement is INCORRECT. Quadrant II points have a negative x and a positive y, so the form is (-, +).
- Quadrant III : (-, +): This statement is INCORRECT. Quadrant III points have a negative x and a negative y, so the form is (-, -).
- On X-axis: (0, ±): This statement is INCORRECT. For any point on the x-axis, the y-coordinate is always 0. The correct form is (±, 0).
- On Y-axis: (±, 0): This statement is INCORRECT. For any point on the y-axis, the x-coordinate is always 0. The correct form is (0, ±).
- Origin (0,0): This statement is CORRECT.
Final Answer: The incorrect options are:
- Quadrant IV : (-, -)
- Quadrant II : (-, -)
- Quadrant III : (-, +)
- On X-axis: (0, ±)
- On Y-axis: (±, 0)