IIT Madras
Mathematics 1
Representation of a Line-1

Representation of a Line-1

A well-defined collection of distinct objects called elements or members.

https://youtu.be/fKUK8xeuWNo

Learning Outcomes

  1. Obtain equations of horizontal and vertical lines on the coordinate plane.
  2. Find the equation of a line in point-slope form and two-points form.

1️⃣ Equations of Horizontal and Vertical Lines

  • Horizontal Lines: These lines run parallel to the $x$-axis. All points on a horizontal line have the same $y$-coordinate.

Equation:

$$ y = c $$

where $ c $ is a constant representing the $y$-value for every point on the line.

Example: $ y = 3 $ represents a horizontal line passing through all points with $ y = 3 $.

  • Vertical Lines: These lines run parallel to the $y$-axis. All points on a vertical line have the same $x$-coordinate.

Equation:

$$ x = k $$

where $ k $ is a constant representing the $x$-value for every point on the line.

Example: $ x = -2 $ is a vertical line passing through all points with $ x = -2 $.

Image:

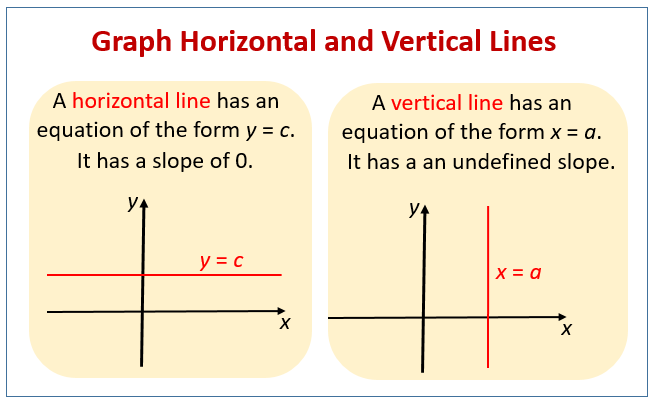
alt text

2️⃣ Find Equation of a Line in Point-Slope Form and Two-Points Form

  • Point-Slope Form Given a point $ (x_1, y_1) $ on the line and the slope $ m $, the equation is:
$$ y - y_1 = m(x - x_1) $$

This form directly relates any point on the line to slope and a reference point.

  • Two-Points Form Given two points $ (x_1, y_1) $ and $ (x_2, y_2) $, the slope is:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

Then the line’s equation can be written as:

$$ \frac{y - y_1}{x - x_1} = \frac{y_2 - y_1}{x_2 - x_1} $$

Image:

alt text alt text

Summary:

  • Horizontal: $ y = c $, Vertical: $ x = k $
  • Point-Slope: uses known point and slope
  • Two-Points: uses two known points

These forms allow flexible calculation and graphing of linear equations.

Exercise Questions 🤯

Hello! On this Wednesday evening here in India, I would be happy to explain these questions about the equations of lines. This is a key area of coordinate geometry.

Question 1: Equation of a Horizontal Line (from file image_0e0a21.png)

The Question: Which of the following represents an equation of the horizontal line?

  • $y = 0$
  • $x = 5$
  • $x = -2$
  • $x = 0$

Core Concept: Equations of Horizontal and Vertical Lines

  • Horizontal Line: A line that runs perfectly flat, parallel to the x-axis. Every single point on this line has the same y-coordinate. Therefore, its equation is always in the form $y = c$, where ‘c’ is that constant y-value.
  • Vertical Line: A line that runs straight up and down, parallel to the y-axis. Every point on this line has the same x-coordinate. Its equation is always in the form $x = c$.

Detailed Solution:

Let’s look at the options:

  • $y = 0$: This equation states that the y-coordinate is always 0, regardless of the x-value. This is the definition of a horizontal line (it’s the x-axis itself).
  • $x = 5$: This is an equation for a vertical line where the x-coordinate is always 5.
  • $x = -2$: This is an equation for a vertical line where the x-coordinate is always -2.
  • $x = 0$: This is an equation for a vertical line where the x-coordinate is always 0 (it’s the y-axis itself).

Final Answer: $y = 0$ represents a horizontal line.

Question 2: Equation of a Line Parallel to the X-axis (from file image_0e0a21.png)

The Question: The equation of a line parallel to the X-axis and passing through the point $(-2, 0)$ is __________.

  • $y=0$
  • $x=0$
  • $x=-2$
  • $y=-2$

Core Concept: Finding the Equation of a Specific Horizontal Line

  1. A line parallel to the X-axis is a horizontal line.
  2. Its equation must be in the form $y = c$.
  3. If the line passes through a specific point $(a, b)$, then the y-coordinate of that point gives us the value of $c$. So, the equation must be $y = b$.

Detailed Solution:

  1. The line is “parallel to the X-axis,” which means it is a horizontal line. Its equation must be $y = c$.
  2. The line “passes through the point $(-2, 0)$”.
  3. This means that for our line, the y-value must be the same as the y-coordinate of this point. The y-coordinate is 0.
  4. Therefore, the constant $c$ is 0, and the equation of the line is $y = 0$.

Final Answer: The equation is $y=0$.

Question 3: Equation from Origin and Slope (from file image_0e0a21.png)

The Question: The equation of a line passing through the origin and with slope -1 is __________.

  • $y=x$
  • $y=-x+1$
  • $y=-x$
  • $y=-x-1$

Core Concept: Slope-Intercept Form

A very useful form for the equation of a line is the slope-intercept form:

$$y = mx + c$$

where $m$ is the slope and $c$ is the y-intercept (the point where the line crosses the y-axis).

Detailed Solution:

  1. Identify the slope: We are given that the slope $m = -1$.
  2. Identify the y-intercept: The line passes through the origin, which is the point $(0, 0)$. The y-intercept is the y-value when x is 0, so the y-intercept $c = 0$.
  3. Substitute into the slope-intercept form:
    • $y = mx + c$
    • $y = (-1)x + 0$
  4. Simplify the equation:
    • $y = -x$

Final Answer: The equation is $y = -x$.

Question 4: Equation from Two Points (from both images)

The Question: The equation of a line passing through the origin and $(-1, -3)$ is __________.

  • $y=3x$
  • $y=-3x+3$
  • $y=-3x$
  • $y = -x/3$

Core Concept: Finding the Equation from Two Points

This is a two-step process:

  1. Find the slope ($m$) using the slope formula: $m = \frac{y_2 - y_1}{x_2 - x_1}$.
  2. Use the slope and one point in the slope-intercept form ($y = mx + c$) to find the equation.

Detailed Solution:

  1. Step 1: Find the slope.

    • Our two points are $(x_1, y_1) = (0, 0)$ and $(x_2, y_2) = (-1, -3)$.
    • $m = \frac{-3 - 0}{-1 - 0} = \frac{-3}{-1} = 3$.

  2. Step 2: Find the equation.

    • We know the slope $m = 3$.
    • Since the line passes through the origin $(0, 0)$, the y-intercept $c = 0$.
    • Substitute into the slope-intercept form $y = mx + c$:
    • $y = (3)x + 0$
    • $y = 3x$

Final Answer: The equation of the line is $y = 3x$.

Question 5: Properties of a Horizontal Line (from file image_0e073c.png)

The Question: Which of the following is/are correct with respect to a horizontal line? (Multiple Select Question)

  • It is parallel to the Y-axis.
  • Point (0, 0) can lie on a horizontal line.
  • The equation of a horizontal line can be $x = a$.
  • Points lying on a horizontal line are of the form $(x, a)$.

Core Concept: Properties of a Horizontal Line

A horizontal line has a constant y-value and a slope of 0. It is parallel to the x-axis and perpendicular to the y-axis.

Detailed Solution:

  1. “It is parallel to the Y-axis.”: FALSE. It is perpendicular to the Y-axis.
  2. “Point (0, 0) can lie on a horizontal line.”: TRUE. The x-axis itself is a horizontal line with the equation $y=0$, and it passes through the origin (0, 0).
  3. “The equation of a horizontal line can be $x = a$.”: FALSE. $x=a$ is the equation for a vertical line. A horizontal line is $y=a$.
  4. “Points lying on a horizontal line are of the form $(x, a)$.”: TRUE. This means that for any x-value, the y-value is always the same constant, ‘a’. This is the definition of a horizontal line.

Final Answer: The correct statements are “Point (0, 0) can lie on a horizontal line” and “Points lying on a horizontal line are of the form (x, a)”.

Question 6: Properties of a Vertical Line (from file image_0e073c.png)

The Question: Which of the following is/are correct with respect to a vertical line? (Multiple Select Question)

  • It is parallel to the X-axis.
  • Points lying on a vertical line are of the form $(a, y)$.
  • Point (0, 0) can lie on a vertical line.
  • The equation of a line can be $y=b$.

Core Concept: Properties of a Vertical Line

A vertical line has a constant x-value and an undefined slope. It is parallel to the y-axis and perpendicular to the x-axis.

Detailed Solution:

  1. “It is parallel to the X-axis.”: FALSE. It is perpendicular to the X-axis.
  2. “Points lying on a vertical line are of the form $(a, y)$.”: TRUE. This means that for any y-value, the x-value is always the same constant, ‘a’. This is the definition of a vertical line.
  3. “Point (0, 0) can lie on a vertical line.”: TRUE. The y-axis itself is a vertical line with the equation $x=0$, and it passes through the origin (0, 0).
  4. “The equation of a line can be $y = b$.”: FALSE. This is the equation for a horizontal line. A vertical line is $x=a$.

Final Answer: The correct statements are “Points lying on a vertical line are of the form (a, y)” and “Point (0, 0) can lie on a vertical line”.

Question 7: Forms of Linear Equations (from file image_0e073c.png)

The Question: Choose the correct option. (Multiple Select Question)

  • The equation of a line in point slope form and two point form can both be converted to $y = mx + c$ form.
  • $(y - y_0) = m(x - x_0)$ is a two point form of equation of line
  • The equation of a horizontal line can be $x=a$
  • $(y - y_1) = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1)$ is a two point form of the equation of a line

Core Concepts: Different Forms of Linear Equations

  • Slope-Intercept Form: $y = mx + c$ (Given slope and y-intercept).
  • Point-Slope Form: $y - y_1 = m(x - x_1)$ (Given a point and the slope).
  • Two-Point Form: $y - y_1 = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1)$ (Given two points). Notice that the fraction part is just the slope formula, so this is really just an extension of the point-slope form.

Detailed Solution:

  1. “The equation of a line in point slope form and two point form can both be converted to $y = mx + c$ form.”: TRUE. By distributing and isolating y, both of these forms can be simplified into the slope-intercept form.
  2. "$(y - y_0) = m(x - x_0)$ is a two point form of equation of line": FALSE. This is the standard definition of the point-slope form.
  3. “The equation of a horizontal line can be $x=a$”: FALSE. This is the equation for a vertical line.
  4. "$(y - y_1) = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1)$ is a two point form of the equation of a line": TRUE. This is the standard definition of the two-point form.

Final Answer: The correct options are “The equation of a line in point slope form and two point form can both be converted to y = mx + c form” and "$(y - y_1) = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1)$ is a two point form of the equation of a line".

Practice_Assignment_2Representation of a Line-2