Slope of a line
A well-defined collection of distinct objects called elements or members.
Learning Outcomes
- Understand the concept of slope of a line.
- Determine the slope of the line.
1️⃣ Understand the Concept of Slope of a Line
The slope of a line measures its steepness and direction in the coordinate plane. It is the ratio of the vertical change (“rise”) to the horizontal change (“run”) between two points on the line.
Mathematically, if two points on the line are $ (x_1, y_1) $ and $ (x_2, y_2) $, the slope $ m $ is:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$- If $ m > 0 $, the line rises from left to right.
- If $ m < 0 $, the line falls from left to right.
- If $ m = 0 $, the line is horizontal.
- If $ m $ is undefined (denominator zero), the line is vertical.
Image:
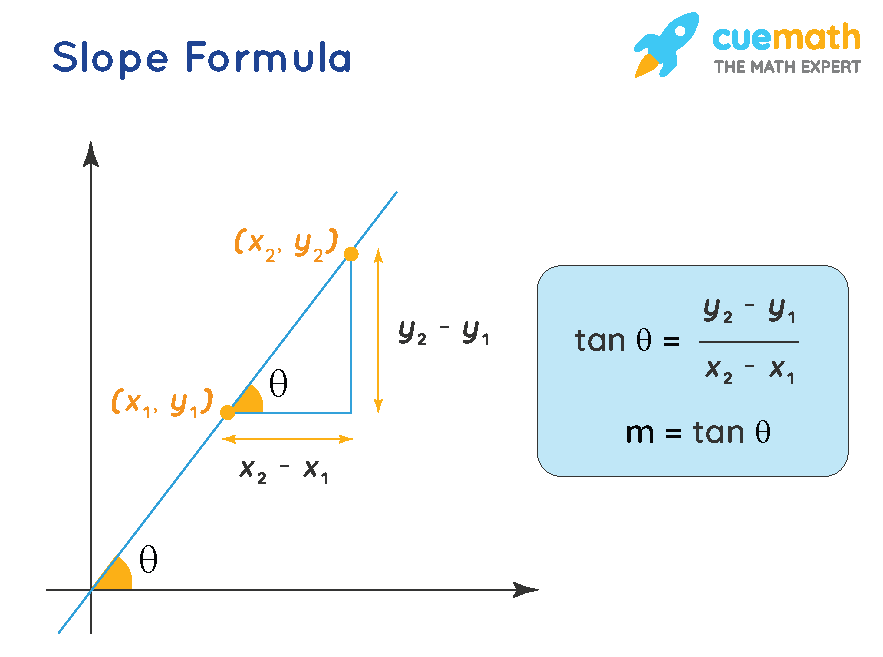
2️⃣ Determine the Slope of a Line
Step-by-step: Given two points $ A(x_1, y_1) $ and $ B(x_2, y_2) $, calculate:
- Find the change in y: $ \Delta y = y_2 - y_1 $
- Find the change in x: $ \Delta x = x_2 - x_1 $
- Compute slope: $ m = \frac{\Delta y}{\Delta x} $
Example: Points $ A(2, 3) $ and $ B(6, 11) $:
$$ \Delta y = 11 - 3 = 8, \quad \Delta x = 6 - 2 = 4 $$$$ m = \frac{8}{4} = 2 $$The slope is 2, indicating the line rises twice as fast vertically for each unit horizontally.
Image:
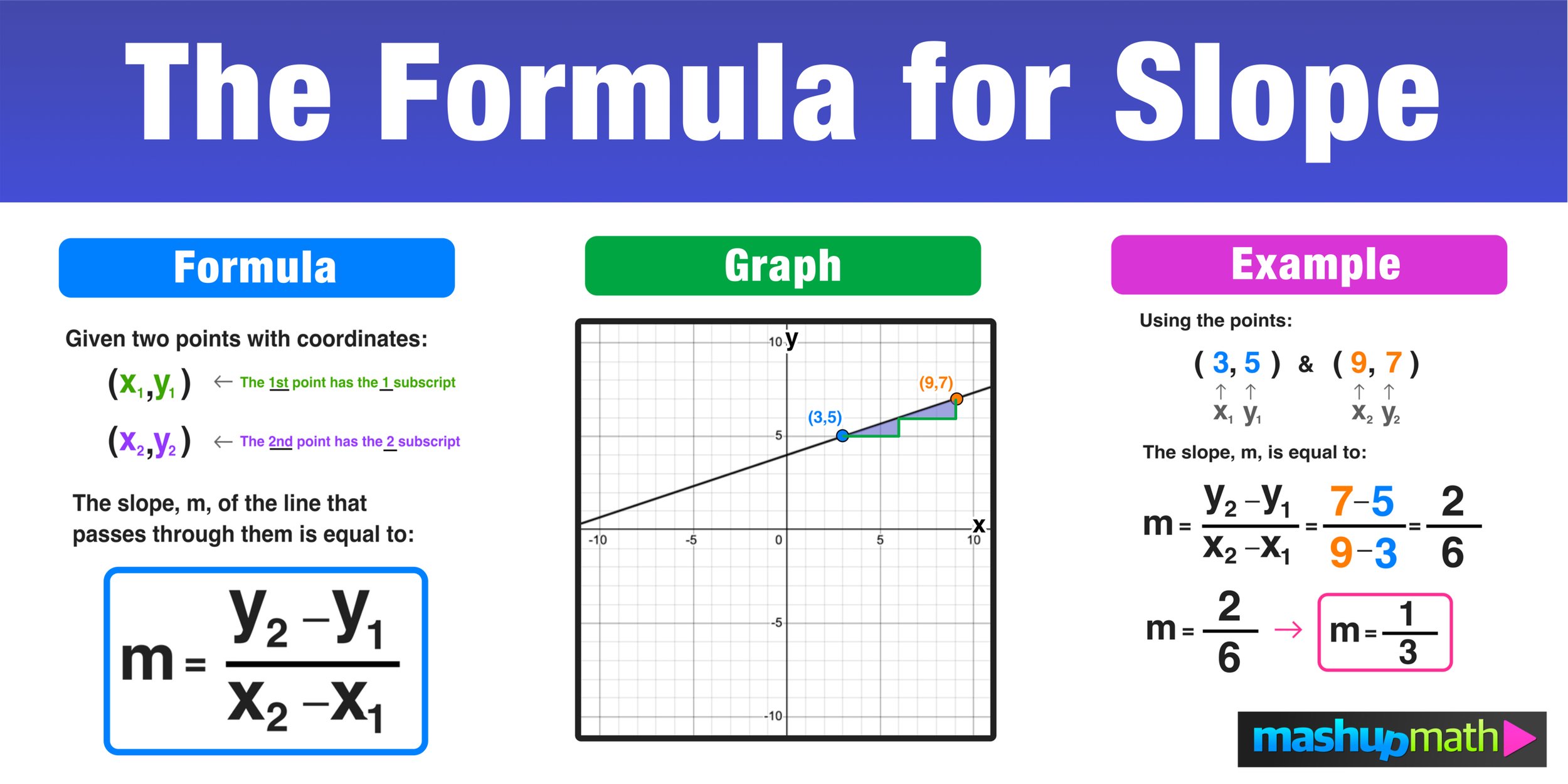
These formulas and visuals help you understand and compute the slope, giving insight into the characteristics of a line in the coordinate system.
Sources:
Exercise Questions 🤯


Hello! On this Wednesday evening here in India, I can certainly help you master the concept of a line’s slope with detailed explanations for each of these questions.
Question 1: Calculating the Slope of a Line
The Question: Find the slope of a line passing through the origin and the point $(-3, -2)$.
- 4/6
- -2/3
- -1/3
- 3/2
Core Concept: The Slope Formula
The slope of a line (often denoted by the letter $m$) is a measure of its steepness. It’s calculated as the ratio of the vertical change (“rise”) to the horizontal change (“run”) between any two points on the line.
For two points, $(x_1, y_1)$ and $(x_2, y_2)$, the slope $m$ is given by the formula:
$$m = \frac{\text{rise}}{\text{run}} = \frac{y_2 - y_1}{x_2 - x_1}$$Detailed Solution:
Identify the two points:
- The first point is the origin: $(x_1, y_1) = (0, 0)$.
- The second point is given: $(x_2, y_2) = (-3, -2)$.
Apply the slope formula:
$$m = \frac{-2 - 0}{-3 - 0}$$Calculate the result:
$$m = \frac{-2}{-3}$$A negative divided by a negative is a positive.
$$m = \frac{2}{3}$$Check the options: The first option is 4/6. If we simplify this fraction by dividing the numerator and denominator by 2, we get $\frac{4 \div 2}{6 \div 2} = \frac{2}{3}$. This matches our result.
Final Answer: The slope is 2/3, which corresponds to the option 4/6.
Question 2: Finding an Unknown Coordinate Using Slope
The Question: If the slope of a line passing through $P(1, 0)$ and $Q(-2, k)$ is 1, then the value of $k$ is __________.
- -2
- -3
- 0
- 2
Core Concept: The Slope Formula (in reverse)
We use the same slope formula, but this time we know the slope ($m$) and need to solve for one of the missing coordinates. We’ll set up an algebraic equation.
Detailed Solution:
Identify the knowns:
- Point 1: $(x_1, y_1) = (1, 0)$.
- Point 2: $(x_2, y_2) = (-2, k)$.
- The slope: $m = 1$.
Set up the equation using the slope formula:
$$m = \frac{y_2 - y_1}{x_2 - x_1}$$$$1 = \frac{k - 0}{-2 - 1}$$Solve the equation for k:
$$1 = \frac{k}{-3}$$Multiply both sides by -3:
$$1 \times (-3) = k$$$$-3 = k$$
Final Answer: The value of $k$ is -3.
Question 3: Properties of Slopes
The Question: Which of the following is/are correct with respect to the slope of a line? (Multiple Select Question)
- The line parallel to the X-axis has slope of value 1
- The slope of a line which is parallel to the Y-axis is not defined
- The line parallel to the Y-axis has a slope of 90
- The line parallel to the X-axis has a slope 0
- The slope of a line is always positive
Core Concepts: Slopes of Horizontal and Vertical Lines
- Horizontal Line (parallel to the x-axis): A horizontal line has no vertical change, or “rise”. Its rise is always 0. Therefore, its slope is $m = \frac{0}{\text{run}} = 0$.
- Vertical Line (parallel to the y-axis): A vertical line has no horizontal change, or “run”. Its run is always 0. Division by zero is mathematically impossible. Therefore, the slope of a vertical line is undefined.
Detailed Solution:
Let’s evaluate each statement:
- “The line parallel to the X-axis has slope of value 1”: This is FALSE. A line parallel to the x-axis is horizontal and has a slope of 0.
- “The slope of a line which is parallel to the Y-axis is not defined”: This is TRUE. A line parallel to the y-axis is vertical, and its slope is undefined.
- “The line parallel to the Y-axis has a slope of 90”: This is FALSE. This confuses the angle of inclination (90 degrees) with the slope. The slope is undefined.
- “The line parallel to the X-axis has a slope 0”: This is TRUE.
- “The slope of a line is always positive”: This is FALSE. A line can have a positive slope (rising left to right), a negative slope (falling left to right), or a zero slope (horizontal).
Final Answer: The two correct statements are “The slope of a line which is parallel to the Y-axis is not defined” and “The line parallel to the X-axis has a slope 0”.
Question 4: Lines with Zero Slope
The Question: Through which of the following points do lines of slope 0 pass? (Multiple Select Question)
- (0, 0)
- (-100, 0.5)
- (-0.05, 0)
- (0, 4)
Core Concept: Horizontal Lines
A line with a slope of 0 is a horizontal line. The equation for any horizontal line is of the form $y = c$, where $c$ is a constant. This means that every single point on that line must have the exact same y-coordinate.
Detailed Solution:
The question can be interpreted as asking, “Which of these points could lie on the same horizontal line?” To answer this, we look for points that share the same y-coordinate.
- Point (0, 0): The y-coordinate is 0.
- Point (-100, 0.5): The y-coordinate is 0.5.
- Point (-0.05, 0): The y-coordinate is 0.
- Point (0, 4): The y-coordinate is 4.
By comparing the y-coordinates, we can see that the points (0, 0) and (-0.05, 0) both have a y-coordinate of 0. Therefore, they both lie on the same horizontal line, which is the x-axis ($y=0$), a line with a slope of 0. The other two points, (-100, 0.5) and (0, 4), lie on different horizontal lines ($y=0.5$ and $y=4$, respectively).
Final Answer: The points (0, 0) and (-0.05, 0) lie on the same line of slope 0.
https://study.com/academy/lesson/calculating-the-slope-of-a-line-point-slope-form-slope-intercept-form-more.html ↩︎
https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:linear-equations-graphs/x2f8bb11595b61c86:slope/a/slope-review ↩︎
https://study.com/academy/lesson/what-is-slope-definition-formulas-quiz.html ↩︎