IITM-Foundation-Course-Mathematics-1

01 Construction of Subsets and set operations

A well-defined collection of distinct objects called elements or members. Learning Outcomes: Write a set in its comprehensive form called set comprehension. Construct different subsets from a given set. Distinguish between closed interval and open interval. Demonstrate the ability to perform operations like union, intersection, set difference, and complement on sets using proper notation. 1️⃣ Set Comprehension: Writing Sets in Comprehensive Form Set comprehension is a way to define a set by describing the properties its members must satisfy instead of listing elements. Notation: $$ A = \{x \mid \text{property of } x\} $$Reads as: “Set $ A $ is the set of all $ x $ such that $ x $ satisfies the property.”

🧮

02 Examples of Set Operations and Counting Problems

A well-defined collection of distinct objects called elements or members. Learning Outcomes: Understand set notations. Solve counting problems using Venn diagrams. Here is a detailed guide covering set notations and solving counting problems using Venn diagrams with 10 examples, including diagrams and emojis to enhance clarity.

🧮

03 Functions

A well-defined collection of distinct objects called elements or members. Learning Outcomes: Define a function, domain, co-domain, and range of a function. Identify the domain and range of a given function. Classify a function as an injective function, a surjective function, both or neither. Define bijection. 1️⃣ Define Function, Domain, Co-domain, and Range Function: A relation $f$ from set $A$ (domain) to set $B$ (co-domain) that assigns each element in $A$ exactly one element in $B$. Denoted as $f: A \to B$. Domain ($A$): The set of input values over which the function is defined. Example: $A = {1,2,3}$. Co-domain ($B$): The set where outputs of the function lie. Example: $B = {a,b,c,d}$. Range: The subset of the co-domain actually mapped by the function. For example, if $f(1) = a, f(2) = b, f(3) = a$, then range $= {a,b}$. Diagram: Function Mapping

📐

04 Mathematics for Data Science 1

IIT Madras has launched the BS in Data Science and Applications. In this program, the course contents are delivered online and can be studied by anyone from anywhere, while the monthly quizzes and final semester exams will have to be attended in-person at designated centres.

📃

05 Natural Numbers and their operations

Of course! Let’s dive deep into the world of Natural Numbers and their operations. We’ll start from the very basics and build up to the properties that govern them. Identifying Natural Numbers and Integers Natural numbers are positive whole numbers, used for counting: 1, 2, 3, 4, 5, ….12 Integers include all positive and negative whole numbers and zero: …, -3, -2, -1, 0, 1, 2, 3, ….3

🧮

06 Rational Numbers

Here is a detailed, emoji-enhanced guide to rational numbers, ordering, GCD, and density, with diagrams and markdown image code for added visuals. Learning Outcomes: Define rational numbers. Order and compare rational numbers. Find the greatest common divisor of two integers. Understand why rational numbers are dense on the number line. 🧮 Define Rational Numbers A rational number is any number that can be written as a fraction $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$.123

🧮

07 Real and Complex Numbers

Real Numbers (R) include all rational numbers plus all irrational numbers (numbers that cannot be expressed as fractions). This makes the real numbers a complete set covering every possible point on the number line. Learning Outcomes: Know how rational numbers extend to real numbers. Identify irrational numbers and complex numbers. Classify a real number as an integer, rational, or irrational number. 1️⃣ How Rational Numbers Extend to Real Numbers Rational Numbers ($\mathbb{Q}$) are numbers expressed as fractions $\frac{p}{q}$, where $p, q$ are integers, $q \neq 0$. Examples: $\frac{1}{2}, 0.75, -3$.12 Real Numbers ($\mathbb{R}$) include all rational numbers plus all irrational numbers (numbers that cannot be expressed as fractions). This makes the real numbers a complete set covering every possible point on the number line.3 Diagram:

🧮

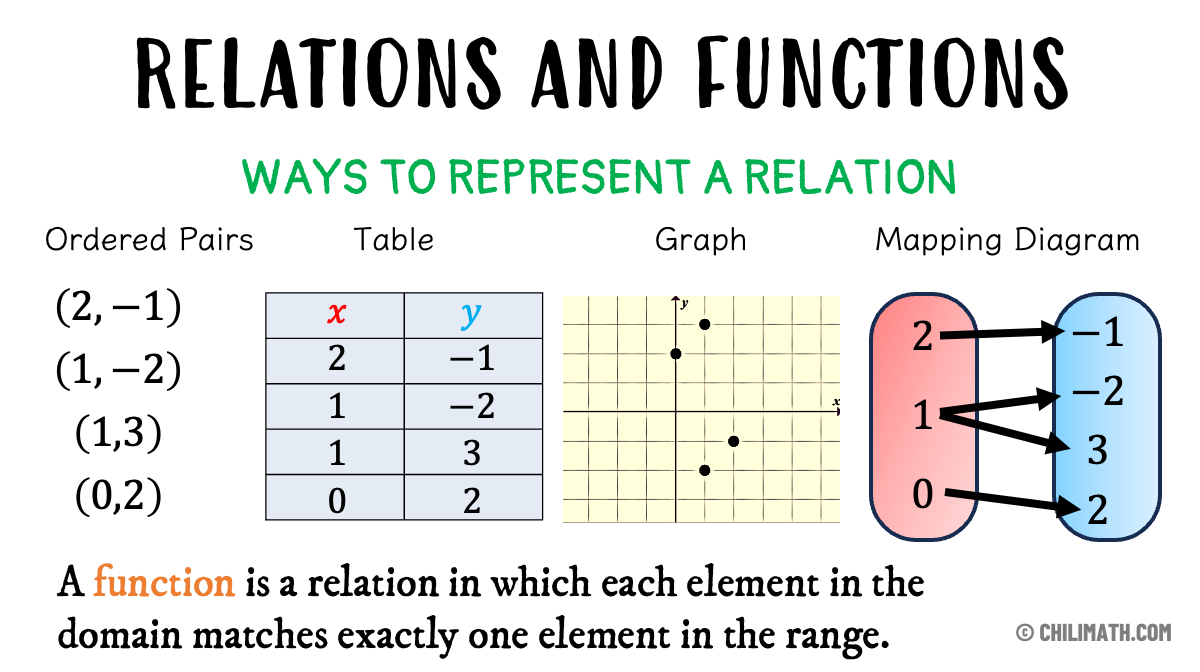08 Relations

A well-defined collection of distinct objects called elements or members. Learning Outcomes: Compute the cartesian product of two non-empty sets. Identify relations as a subset of the cartesian product. List the properties of relations like reflexive, symmetric, transitive, and antisymmetric. Define equivalence relation and equivalence classes. 1️⃣ Compute the Cartesian Product of Two Non-Empty Sets Definition: The Cartesian Product $ A \times B $ of sets $ A $ and $ B $ is the set of all ordered pairs $(a, b)$ such that $a \in A$ and $b \in B$. $$ A \times B = \{ (a, b) \mid a \in A, b \in B \} $$ Example: $ A = {1, 2}, B = {x, y} $ Then: $$ A \times B = \{(1,x), (1,y), (2,x), (2,y)\} $$ Diagram: Cartesian Product

🧮

09 Set Examples

A well-defined collection of distinct objects called elements or members. Learning Outcomes: Describe the membership of sets. Recognize that set comprehension combines generators, filters, and transformations to produce new sets from old sets. 1️⃣ Describe the Membership of Sets Membership refers to whether an element belongs to a set or not. Notation: If $x$ is an element of set $A$, we write: $$ x \in A $$pronounced as “$x$ belongs to $A$.” - If $x$ is not an element of $A$, write:

🧮

10 Set Theory

A well-defined collection of distinct objects called elements or members. Learning Outcomes: Define a set, cardinality of a set, subset, proper subset, power set, and empty set, using proper notations. Interpret a Venn diagram as a visual representation of a set. Explain why a set with n elements has 2 n subsets. 1️⃣ Define Set Concepts with Notations Set ( $ A $ ): A well-defined collection of distinct objects called elements or members. Example: $ A = {1, 2, 3, 4} $ 📦 Think of it as a box containing elements. Cardinality ( $ |A| $ ): The number of elements in set $ A $. Example: If $ A = {1, 2, 3} $, then $ |A| = 3 $. 🔢 Counts how many items are in the set. Subset ( $ B \subseteq A $ ): Set $ B $ is a subset of $ A $ if every element of $ B $ is also in $ A $. Example: $ B = {1, 2} \subseteq A = {1, 2, 3} $. 🤝 Everything in $ B $ is in $ A $. Proper Subset ( $ B \subset A $ ): $ B $ is a subset of $ A $, but $ B \neq A $. Example: $ B = {1, 2} \subset A = {1, 2, 3} $. 🚫 $ B $ does not contain all elements of $ A $. Power Set ( $ \mathcal{P}(A) $ ): The set of all subsets of $ A $, including the empty set and $ A $ itself. Example: For $ A = {1, 2} $, $ \mathcal{P}(A) = {\emptyset, {1}, {2}, {1,2}} $. 📚 All possible collections you can make from the set. Empty Set ( $ \emptyset $ ): The set with no elements. Example: $ \emptyset = {} $. ❌ A box with nothing inside. Diagram illustrating sets and subsets:

🧮

11 Relations examples

A well-defined collection of distinct objects called elements or members. Learning Outcomes: List the number of elements in the cartesian product of two finite sets. Interpret relations as a subset of the cartesian product. Represent data tables as relations. Exercise Questions

🧮

12 Functions Examples

A well-defined collection of distinct objects called elements or members. https://youtu.be/6YrUx0bAnuQ Learning Outcomes: Find the domain and range of a given function. Understand what is the maximum value, minimum value of a function. Understand local maximum and local minimum. Identify whether one function grows faster than another. Exercise Questions

🧮

13 Prime Numbers

A well-defined collection of distinct objects called elements or members. https://youtu.be/98NeCye2i3k Learning Outcomes: Argue why the set of prime numbers is infinite. Identify if a given number is prime or not.

🧮

14 Why is a number irrational?

A well-defined collection of distinct objects called elements or members. https://youtu.be/xUZeskT6WiQ Learning Outcomes: Understand why root 2 is an irrational number. Explain why not every number can be expressed in p/q form.

🧮

15 Set versus Collections

A well-defined collection of distinct objects called elements or members. https://youtu.be/kM9nVJks1a8 Learning Outcomes: Express natural numbers as sets. Understand Russell’s paradox (why not every collection can be called a set). Define class.

🧮

16 Degrees of infinity

A well-defined collection of distinct objects called elements or members. https://youtu.be/yjJ_pualJr4 Learning Outcomes: Compare the cardinalities of two infinite sets. Know what countable sets are. Explain why the cardinalities of N,Z, and Q are the same. Argue that the real numbers are not countable.

🧮

17 Week 1 | Practice Assignemnt

Question 1: Venn Diagram Interpretation (from file image_5c141c.png) The Question: Given below is a Venn diagram for sets of students who take Maths, Physics, and Statistics. Which of the option(s) is (are) correct? [Venn diagram shows three overlapping circles: Maths (regions A, D, G, F), Physics (regions B, E, G, F), and Statistics (regions C, D, G, E)] D is the set of students who take both Maths and Statistics. $D \cup E \cup F \cup G$ is the set of all students who take at least two subjects. E is a subset of the set of the students who have not taken Maths. $Maths \setminus D$ is the set of all students who have taken only Maths. $Physics \setminus (D \cup G \cup E)$ is the set of all students who have taken only Physics. Core Concepts: Set Operations in Venn Diagrams

🧮

18 Week 1 | Graded Assignment

Question 1: Irrational Numbers The Question: Which of the following are irrational numbers? 2.99999999 $(\sqrt{8} + \sqrt{2})(\sqrt{12} - \sqrt{3})$ $\frac{\sqrt{8} + \sqrt{2}}{\sqrt{8} - \sqrt{2}}$ $\frac{\sqrt{6} + \sqrt{3}}{\sqrt{6} - \sqrt{3}}$ Core Concepts: Rational vs. Irrational Numbers Rational Number: Expressible as fraction $p/q$, where $p,q$ are integers, $q \ne 0$. Decimals terminate or repeat. Irrational Number: Cannot be expressed as a simple fraction. Decimals non-terminating and non-repeating. Detailed Solution:

🧮

19 Rectangular Coordinate system

A well-defined collection of distinct objects called elements or members. https://youtu.be/RfG2NLXqGE8 Learning Outcomes Know the basics of the rectangular coordinate system and the quadrants. Recognize, show, or plot a point on the coordinate plane. 1️⃣ Basics of the Rectangular Coordinate System and Quadrants The rectangular coordinate system (also called the Cartesian coordinate system) uses two number lines that intersect at right angles at a point called the origin (0,0).

🧮

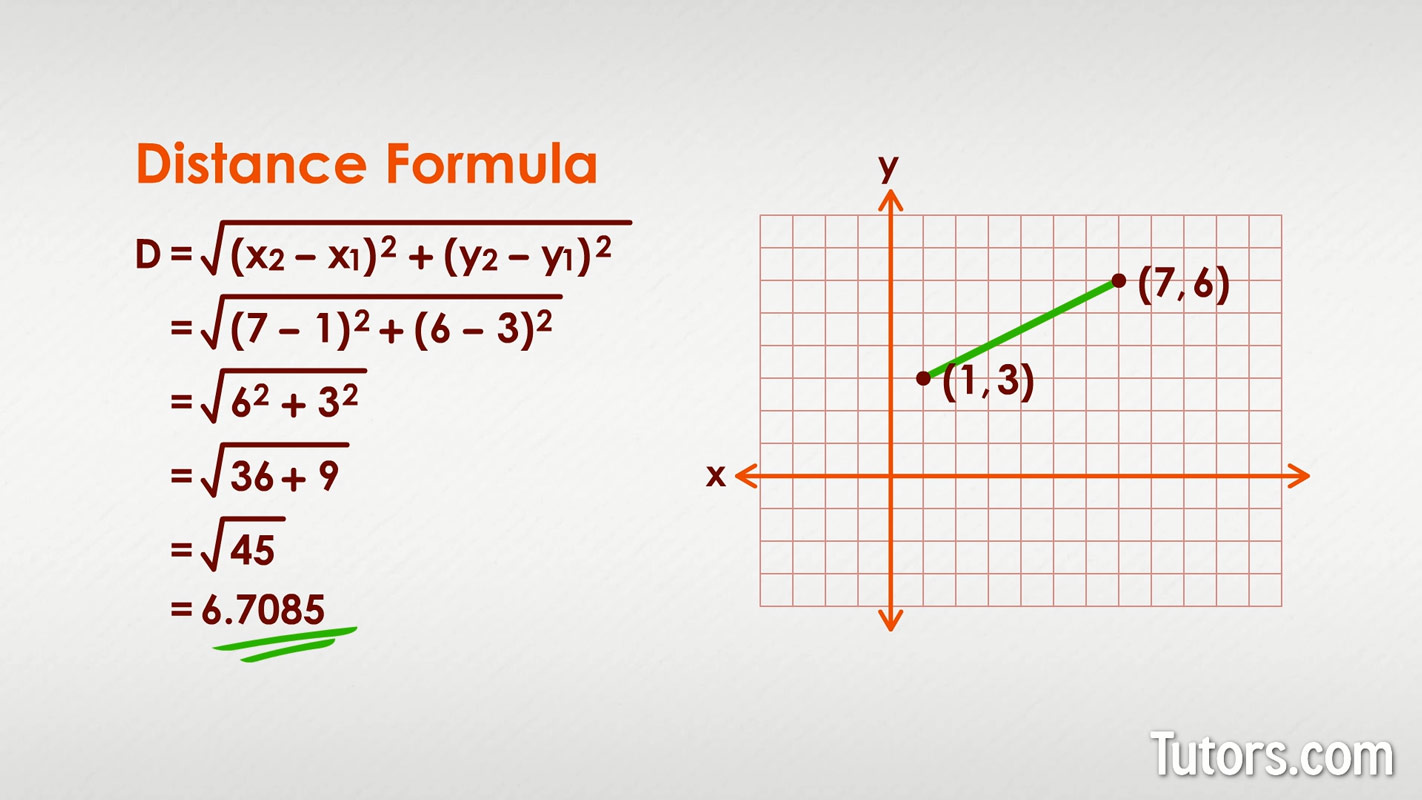20 Distance formula

A well-defined collection of distinct objects called elements or members. https://youtu.be/aDhyAkXiDOY Learning Outcomes Compute the distance of a point from the origin in the rectangular coordinate system. Derive a general distance formula between any two points on the coordinate plane. 1️⃣ Distance of a Point from the Origin To compute the distance of a point $P(x, y)$ from the origin $(0, 0)$ in the rectangular coordinate system, use the distance formula:

🧮

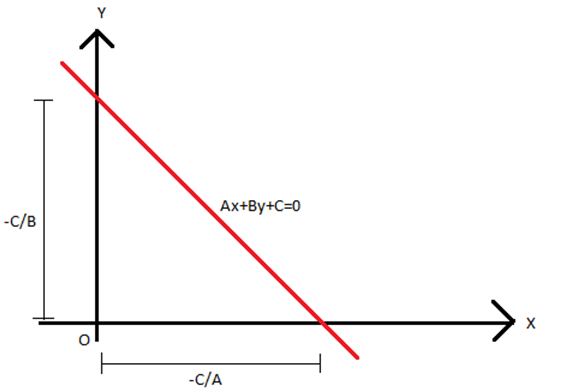
21 Distance of a line from a given point

A well-defined collection of distinct objects called elements or members. https://youtu.be/tYSZ4L0X3kY Learning Outcomes ● Explain the concept of intercepts of a line on the axes. ● Calculate the distance of a point from a line using the general linear expression. ● Determine the distance between two parallel lines.

🧮

22 Equation of a perpendicular line passing through a point

A well-defined collection of distinct objects called elements or members. https://youtu.be/CjeHgCXhi4k Learning Outcomes ● Find the general equation of a line passing through a point and is perpendicular to a given line.

🧮

23 Equation of parallel and perpendicular lines in general form

A well-defined collection of distinct objects called elements or members. https://youtu.be/gJuJtTYmbSs Learning Outcomes ● Determine the general conditions for the slope of a line parallel or perpendicular to a given line. ● Find the general equation of a line parallel or perpendicular to a given line.

🧮

24 General equation of line

A well-defined collection of distinct objects called elements or members. https://youtu.be/_3Iidm8NnbM Learning Outcomes ● Understand the general equation of a line. ● Find the different forms of the equation of a line including slope-point form, slope-intercept form, two-point form and intercept form from the general linear equation.

🧮

25 Practice_Assignment_2

A well-defined collection of distinct objects called elements or members. Week 02 - Tutorial 01 https://youtu.be/ggpFtRiDUFA Week 02 - Tutorial 02 https://youtu.be/Qr7Kou01yj8

🧮

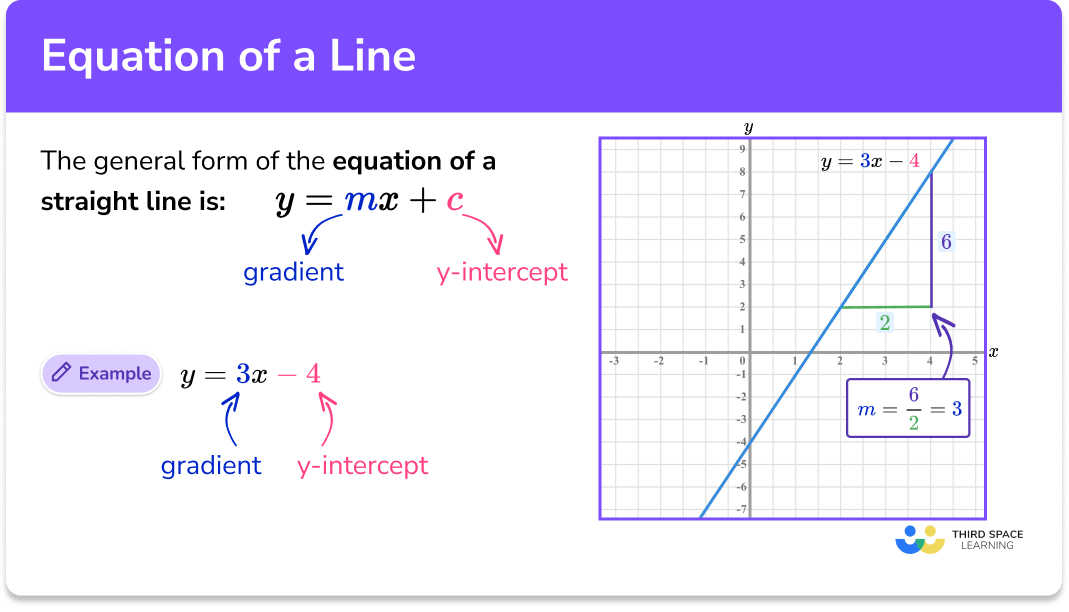26 Representation of a Line-1

A well-defined collection of distinct objects called elements or members. https://youtu.be/fKUK8xeuWNo Learning Outcomes Obtain equations of horizontal and vertical lines on the coordinate plane. Find the equation of a line in point-slope form and two-points form. 1️⃣ Equations of Horizontal and Vertical Lines Horizontal Lines: These lines run parallel to the $x$-axis. All points on a horizontal line have the same $y$-coordinate. Equation:

🧮

27 Representation of a Line-2

A well-defined collection of distinct objects called elements or members. https://youtu.be/zM0q4y-y4so Learning Outcomes Find the equation of a line in slope-intercept form and intercept form. Exercise Questions

🧮

28 Straight line fit

A well-defined collection of distinct objects called elements or members. https://youtu.be/xdZHsFuyBZM Learning Outcomes ● Associate the study on lines with real-world problems. ● Predict the suitable line among the given set of lines for a given set of points. ● Find the best fit line among the given set of lines using the Sum Squared Error Method for a given data.

🧮

29 Section formula

A well-defined collection of distinct objects called elements or members. https://youtu.be/B5yv8zPrkek Learning Outcomes Find the ratio in which a point divides a line segment. Derive the section formula to find the coordinate of a point that divides a line segment. 1. Finding the Ratio in Which a Point Divides a Line Segment Suppose you have points $ A(x_1, y_1) $ and $ B(x_2, y_2) $, and a third point $ P(x, y) $ somewhere between them (or on the extension), and you want to know the ratio $ m:n $ in which $ P $ divides $ AB $.

🧮

30 Area of triangle

A well-defined collection of distinct objects called elements or members. https://youtu.be/x62fodF7ezk Learning Outcomes Compute the area of a trapezium. Compute the area of a triangle using coordinates of its vertices. 1️⃣ Compute the Area of a Trapezium A trapezium (or trapezoid) is a quadrilateral with at least one pair of parallel sides called the bases.

🧮

31 Parallel and perpendicular lines

A well-defined collection of distinct objects called elements or members. https://youtu.be/CXhBGVfmtBg Learning Outcomes Explain why the slope of a line does not uniquely determine the line. Characterize parallel and perpendicular lines using the slope. Compute the angle between 2 lines using their slopes. 1️⃣ Why the Slope of a Line Does Not Uniquely Determine the Line The slope measures the steepness and direction of a line but does not uniquely determine a line by itself.

🧮

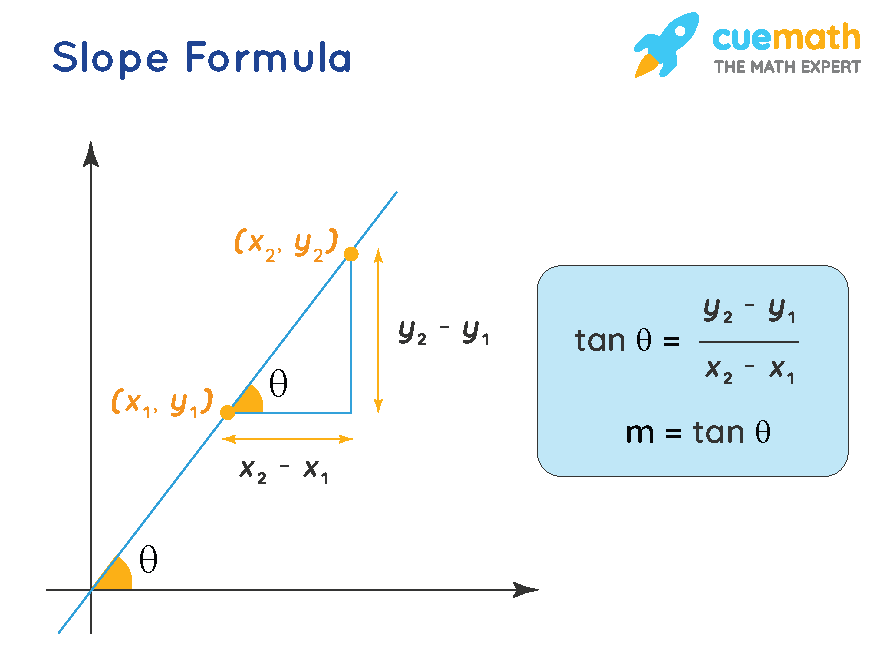32 Slope of a line

A well-defined collection of distinct objects called elements or members. https://youtu.be/V-b3BL8DAvU Learning Outcomes Understand the concept of slope of a line. Determine the slope of the line. 1️⃣ Understand the Concept of Slope of a Line The slope of a line measures its steepness and direction in the coordinate plane. It is the ratio of the vertical change (“rise”) to the horizontal change (“run”) between two points on the line.

🧮

33 Graded Assignment 2

Graded Assignment - 2 solution

🧮

34 Quadratic functions

A well-defined collection of distinct objects called elements or members. https://youtu.be/U4gr4zMosMk Learning Outcomes Compare quadratic functions and linear functions. Define a quadratic function and represent it using a parabola. Identify different terms in a quadratic function and comprehend the importance of their coefficients. Represent the ‘axis of symmetry’ and ‘vertex’ used to represent parabola. Exercise Questions 🤯

🧮

35 Examples of Quadratic functions

A well-defined collection of distinct objects called elements or members. https://youtu.be/dvJKbgIPG8Q Learning Outcomes Determine the minimum and maximum value of a quadratic function. Explain the concept of range and domain of a quadratic function. Demonstrate the ability to apply these concepts in real life scenarios. Exercise Questions 🤯

🧮

36 Quadratic

A well-defined collection of distinct objects called elements or members.

🧮

37 Quadratic

A well-defined collection of distinct objects called elements or members.

🧮

38 Quadratic formula

A well-defined collection of distinct objects called elements or members. https://youtu.be/1shGS3xfmwc Learning Outcomes The student can solve quadratic equations with irrational roots. The student will be able to solve the quadratic equation using the quadratic formula. The student can choose the appropriate method to solve a quadratic equation. The student can appreciate the use of discriminant in finding the nature of roots for quadratic equations. The student can understand the concept of the ‘axis of symmetry’. Exercise Questions 🤯

🧮

39 Slope | Line & Parabola

A well-defined collection of distinct objects called elements or members. https://youtu.be/kaByg1VQxqk Exercise Questions 🤯 Hello! On this Wednesday evening here in India, I’d be happy to guide you through these questions. They are great examples of how the concepts of parabolas and their slopes (derivatives) are applied in different scenarios.

🧮

40 Slope of quadratic function

A well-defined collection of distinct objects called elements or members. https://youtu.be/1_Y2cZMrcfY Learning Outcomes Define the slope of a quadratic function. Compute the slope of any given parabola. Differentiate between slopes of linear equations and slopes of quadratic equations. Exercise Questions 🤯

🧮

41 Solution of quadratic equation using Factorization

A well-defined collection of distinct objects called elements or members. https://youtu.be/ZRXWkzFSZzU Learning Outcomes The student will be able to solve the quadratic equation in an algebraic manner using factorization. Students can identify the intercept form of the quadratic equation and convert the intercept form into the normal form. Exercise Questions 🤯

🧮

42 Solution of quadratic equation using graph

A well-defined collection of distinct objects called elements or members. https://youtu.be/RzIBZbGov4w Learning Outcomes Define the standard form of quadratic equations and relate this with the quadratic function. Compute roots of equations and zeros of a function. Solve quadratic equations using the graphing technique. Exercise Questions

🧮

43 Solution of quadratic equation using Square method

A well-defined collection of distinct objects called elements or members. https://youtu.be/qvUX-jgtogg Exercise Questions 🤯 Hello! On this Wednesday evening here in India, I’d be happy to explain these questions. They all revolve around a very powerful technique for working with quadratic equations called “Completing the Square”.

🧮

44 Summary Lecture (Quadratic Functions)

A well-defined collection of distinct objects called elements or members. https://youtu.be/JkbFTVFw1yQ

🧮

45 Graded Assignment 3

A well-defined collection of distinct objects called elements or members.

🧮

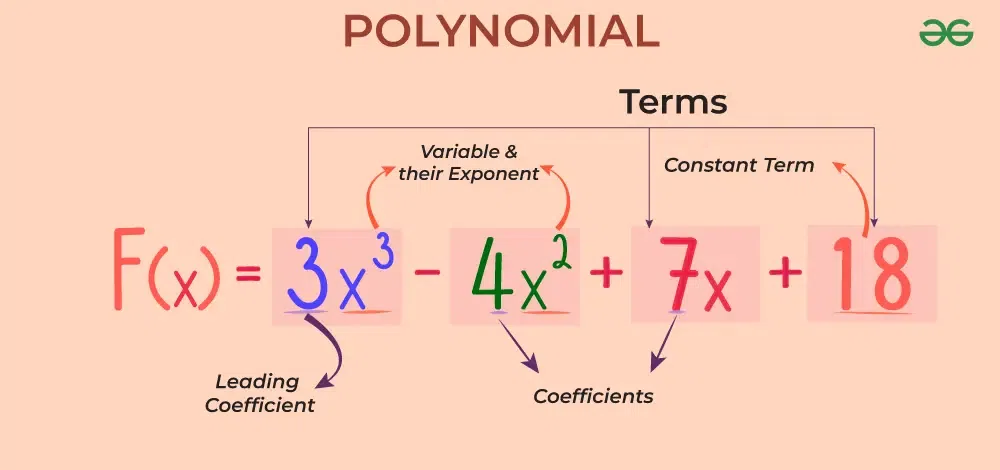46 Polynomials

A well-defined collection of distinct objects called elements or members. https://youtu.be/2PTcxG8e6os Learning Outcomes Define a polynomial. Distinguish between a layman’s perspective and a mathematician’s perspective about a polynomial. Understand the origin of the word ‘polynomial’. Identify if a given function is a polynomial or not. Identify types of polynomials based on the number of variables.

🧮

47 Algebra of polynomials - Addition & Subtraction

A well-defined collection of distinct objects called elements or members. https://youtu.be/KJXkTzKAZ6k Learning Outcomes Understand n-degree polynomials of one variable. Compute the sum of polynomials. Compute the difference between polynomials.

🧮

48 Algebra of polynomials - Division

A well-defined collection of distinct objects called elements or members. https://youtu.be/2eWP19N8wn4 Learning Outcomes Compute the quotient and remainder from division of one polynomial by another. Determine the feasibility of division of polynomials based on degrees of numerator and denominator.

🧮

49 Algebra of polynomials - Multiplication

A well-defined collection of distinct objects called elements or members. https://youtu.be/WOqISzw8jYs Learning Outcomes Compute the product of two general polynomials using corresponding coefficients. Exercise Questions 🤯

🧮

50 Degree of Polynomials

A well-defined collection of distinct objects called elements or members. https://youtu.be/s9zDRWmgsb4 Learning Outcomes Define the degree of a polynomial. Understand the degree of zero polynomial. Classify polynomials based on degrees of polynomials.

🧮

51 Division Algorithm

A well-defined collection of distinct objects called elements or members. https://youtu.be/Y1_T6augNFo Learning Outcomes Describe four steps of algorithm for long division of polynomials with corresponding examples.

🧮

52 Graphs of Polynomials - Behavior at X-intercepts

A well-defined collection of distinct objects called elements or members. https://youtu.be/1t4-35dKUno Learning Outcomes  Explain the graphical behavior of a polynomial at X-intercepts with examples.

🧮

53 Graphs of Polynomials - End behavior

A well-defined collection of distinct objects called elements or members. https://youtu.be/cggv0rx2yBo Learning Outcomes  Visualize the end behavior of a polynomial from its algebraic expression depending on the degree and leading coefficient of the polynomial.  Compare the end behavior of the graph of a polynomial with the end behavior of its algebraic expression.

🧮

54 Graphs of Polynomials - Graphing & Polynomial creation

A well-defined collection of distinct objects called elements or members. https://youtu.be/6IVf5Af1nO0 Learning Outcomes  List out the steps of graphing a polynomial.  Understand the Intermediate Value theorem.  Know methods to derive the formula from the given graph of a polynomial.

🧮

55 Graphs of Polynomials - Identification and Characterization

A well-defined collection of distinct objects called elements or members. https://youtu.be/5M_oX0EjiEk Learning Outcomes  Identify the graph of a polynomial.  List out the properties of the graph of a polynomial function.

🧮

56 Graphs of Polynomials - Turning points

A well-defined collection of distinct objects called elements or members. https://youtu.be/8a--SspXSXU Learning Outcomes  Define the turning point.  Understand the relationship between the degree of a polynomial and the number of the turning points.

🧮

57 Graphs of Polynomials | Multiplicities

A well-defined collection of distinct objects called elements or members. https://youtu.be/-flkMRCNTPE Learning Outcomes  Visualize the graphical behavior of a polynomial from its algebraic expression.  Identify zeros and their multiplicities of a polynomial from its graph.  Identify the properties of the graph of a polynomial for even degree factor, odd degree factor, and linear factor.  Find the Y-intercept of a polynomial from the algebraic expression.

🧮

58 Polynomials

A well-defined collection of distinct objects called elements or members.

🧮

59 Zeroes of Polynomial Functions

A well-defined collection of distinct objects called elements or members. https://youtu.be/-E21FQ567F8 Learning Outcomes  Identify zeros of a polynomial function.  Demonstrate the methods to factorize polynomials.  Find the zeros and X-intercepts of polynomial functions by factoring.

🧮

60 Graded Assignment 4

Graded Assignment - 4 solution](https://drive.google.com/file/d/10E0_BPD-S_cWdLgj5iTZkR7AhbBaAsRu/view)

🧮

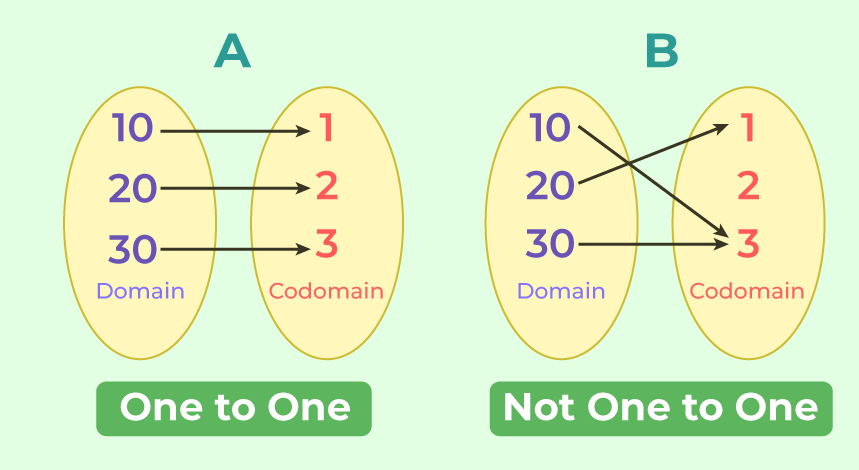61 One-to-One Function | Definition & Tests

A well-defined collection of distinct objects called elements or members. https://youtu.be/CiZrP2-cpGM Learning Outcomes: The student will be able to (a) Perform vertical line test and horizontal line test to find whether a given relation is function or not. (b) Understand reversibility of a function. (c) Properly define one-to-one function.

🧮

62 One-to-One Function - Examples & Theorems

A well-defined collection of distinct objects called elements or members. https://youtu.be/em8Lw7g776M Learning Outcomes: The student will be able to (a) Understand one-to-one functions using examples. (b) Describe increasing and decreasing functions. (c) Identify the class of functions that are one-to-one.

🧮

63 Exponential Functions - Definitions

A well-defined collection of distinct objects called elements or members. https://youtu.be/0l47NHJy-f4 Learning Outcomes: The student will be able to (a) Know the laws of exponents. (b) Define exponential function in standard form. (c) Understand the conditions for base and exponents.

🧮

64 Composite Functions

A well-defined collection of distinct objects called elements or members. https://youtu.be/T4Q2bg0jQZ8 Learning Outcomes: The student will be able to (a) Define Composite function. (b) Understand the practical application of composite function. (c) Identify the domain of a composite function.

🧮

65 Composite Functions - Domain

A well-defined collection of distinct objects called elements or members. https://youtu.be/5u1OlsxuJnw Learning Outcomes: The student will be able to determine the domain for a composite function.

🧮

66 Composite Functions - Examples

A well-defined collection of distinct objects called elements or members. https://youtu.be/QfO-gh-Fpts Learning Outcomes: The student will be able to find the composite function of two given functions.

🧮

67 Exponential

A well-defined collection of distinct objects called elements or members. https://youtu.be/dMvBjIeJe80 Learning Outcomes: The student will be able to (a) Understand the behaviour of exponential functions via graphs. (b) Find the domain, range, intercepts, asymptotes, increasing or decreasing, end behaviour of exponential functions.

🧮

68 Exponential Functions - Graphing

A well-defined collection of distinct objects called elements or members. https://youtu.be/dMvBjIeJe80 https://youtu.be/dMvBjIeJe80 Learning Outcomes: The student will be able to (a) Understand the behaviour of exponential functions via graphs. (b) Find the domain, range, intercepts, asymptotes, increasing or decreasing, end behaviour of exponential functions.

🧮

69 Inverse functions

A well-defined collection of distinct objects called elements or members. https://youtu.be/BpoWKCrLm14 Learning Outcomes: The student will be able to (a) Define Inverse of a function. (b) Find the domain and range of inverse functions.

🧮

70 Natural Exponetial Function

A well-defined collection of distinct objects called elements or members. https://youtu.be/d_LJM7F33uo Learning Outcomes: The student will be able to (a) Understand why is ‘e’ so important? (b) Know the use of natural exponential function. (c) Identify the graph of natural exponential function and its properties.

🧮

71 Graded_assignment_5

Graded assignment week 5 solution

🧮

72 Logarithmic Equations

A well-defined collection of distinct objects called elements or members. https://youtu.be/bB1um2s0NDE Learning Outcomes: To solve different logarithmic equations and numerical examples based on the rules and laws of logarithm with the same bases and different bases. Exercise Questions 🧠

🧮

73 Logarithmic Functions

A well-defined collection of distinct objects called elements or members. https://youtu.be/G5A7imv2Otc Learning Outcomes: To learn inverse of an exponential function and understand its properties Learn ‘7-rule’ Understand the domain and range of exponential functions and logarithmic functions Solve problems on domains and ranges of exponential functions and logarithmic functions To plot graph of inverse function of exponential functions Exercise Questions

🧮

74 Logarithmic Functions

🧮

75 Logarithmic Functions Properties - 1

A well-defined collection of distinct objects called elements or members. https://youtu.be/0WQFcv-wjiI Learning Outcomes: To understand the properties of logarithmic functions To learn the laws of logarithm and corresponding proofs Exercise Questions 🧠

🧮

76 Logarithmic Functions - Graphs

A well-defined collection of distinct objects called elements or members. https://youtu.be/NL8MlTO-Yf8 Learning Outcomes: To plot graph of different logarithmic functions To define natural logarithmic functions Exercise Questions

🧮

77 Logarithmic Functions Applications

A well-defined collection of distinct objects called elements or members. https://youtu.be/XSJ1QZ0MHOs Learning Outcomes: To learn the applications of laws of logarithm Exercise Questions

🧮

78 Logarithmic Functions Properties - 2

A well-defined collection of distinct objects called elements or members. https://youtu.be/eMt8xq0Fuww Learning Outcomes: To learn the theorem of logarithm To apply the ‘Change of base’ rule To understand the proof of the ‘Change of base’ rule To solve different numerical examples based on the aforementioned rules, laws and theorems Exercise Questions 🧠

🧮

79 Solving Exponential Equations

A well-defined collection of distinct objects called elements or members. https://youtu.be/Q5ef_uFX7ug Learning Outcomes: To solve different exponential equations Exercise Questions

🧮

80 Graded_assignment_6

Week 6 graded assignment solution

🧮

81 Functions of one variable

A well-defined collection of distinct objects called elements or members. https://youtu.be/G69JB5310vA Exercise Questions

🧮

82 Graphs and tangents of functions of one variable

A well-defined collection of distinct objects called elements or members. https://youtu.be/EIwT-ibJ7bA Exercise Questions

🧮

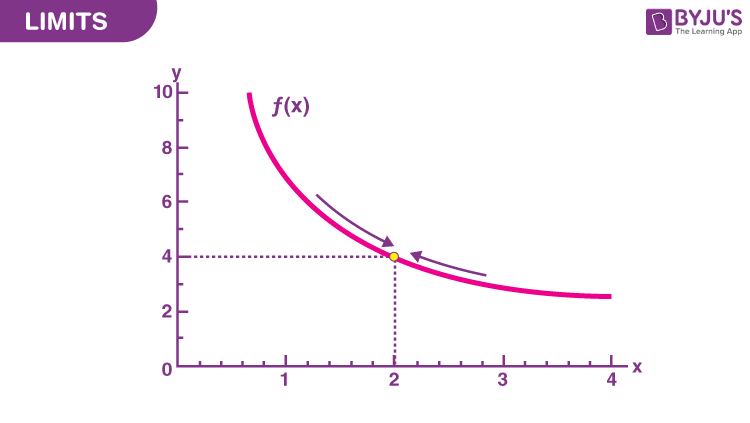
83 Limits

A well-defined collection of distinct objects called elements or members. https://youtu.be/0WHixZdnxTQ Learning Outcomes: To learn inverse of an exponential function and understand its properties Learn ‘7-rule’ Understand the domain and range of exponential functions and logarithmic functions Solve problems on domains and ranges of exponential functions and logarithmic functions To plot graph of inverse function of exponential functions

🧮

84 Limits for functions of one variable

A well-defined collection of distinct objects called elements or members. https://youtu.be/wXPoDGuv1wM Exercise Questions

🧮

85 Limits for sequences

A well-defined collection of distinct objects called elements or members. https://youtu.be/1uySBjXUR1k Exericse Questions Good morning! Here in India on this Monday, let’s work through this excellent set of questions covering the mathematical concept of sequences and their limits. This topic is a cornerstone of calculus and higher mathematics.

🧮

86 LimSome topics from maths 1its

A well-defined collection of distinct objects called elements or members. https://youtu.be/0WHixZdnxTQ https://youtu.be/0WHixZdnxTQ Exercise Questions 🧠

🧮

87 Graded_Assignment_7

Graded assignment week 7-Solution

🧮

88 Computing derivatives and L'Hôpital's rule

A well-defined collection of distinct objects called elements or members. https://youtu.be/Ah3laZhgHus Exercise Questions Good morning! Here in India on this Monday, this is an excellent set of questions that dives deep into the core of differential calculus. We’ll be covering differentiation rules, the powerful L’Hôpital’s rule for limits, and some interesting theoretical properties of derivatives.

🧮

89 Derivatives, tangents, and linear approximation

A well-defined collection of distinct objects called elements or members. https://youtu.be/4IpVR6QpBok Exercise Questions Good morning! Here in India on this Monday, this is a fantastic set of questions that explores one of the most important applications of derivatives: tangent lines and linear approximations.

🧮

90 Differentiability and the derivative

A well-defined collection of distinct objects called elements or members. https://youtu.be/w8R2RdS6xQ4 Exercise Questions

🧮

91 Limits and continuity

A well-defined collection of distinct objects called elements or members. https://youtu.be/do-iDBxQCpw https://youtu.be/do-iDBxQCpw Exercise Questions

🧮

92 Limits and continuity

A well-defined collection of distinct objects called elements or members. https://youtu.be/do-iDBxQCpw

🧮

93 Graded_Assignment_8

A well-defined collection of distinct objects called elements or members. https://youtu.be/do-iDBxQCpw

🧮

94 Computing areas

A well-defined collection of distinct objects called elements or members. https://youtu.be/ZehrWVYoJ_s Exercise Questions 🧠

🧮

95 Computing areas using integrals

A well-defined collection of distinct objects called elements or members. https://youtu.be/79YBSjrg19w Exercise Questions 🧠

🧮

96 Critical points | local maxima and minima

A well-defined collection of distinct objects called elements or members. https://youtu.be/wUPkaBwF1-Y Exercise Questions

🧮

97 Critical points | local maxima and minima

A well-defined collection of distinct objects called elements or members. https://youtu.be/wUPkaBwF1-Y

🧮

98 Examples - Computing Maxima and Minima

A well-defined collection of distinct objects called elements or members. https://youtu.be/LvCh7GTke2E Exercise Questions 🧠

🧮

99 Integrals as anti-derivatives

A well-defined collection of distinct objects called elements or members. https://youtu.be/EeE-4Tp2yGA Exercise Questions

🧮

100 Riemann sums and the integral

A well-defined collection of distinct objects called elements or members. https://youtu.be/qEZiq3QQBok Exercise Questions 🧠

🧮

101 Graded_Assignment_9

A well-defined collection of distinct objects called elements or members. https://youtu.be/wUPkaBwF1-Y

🧮

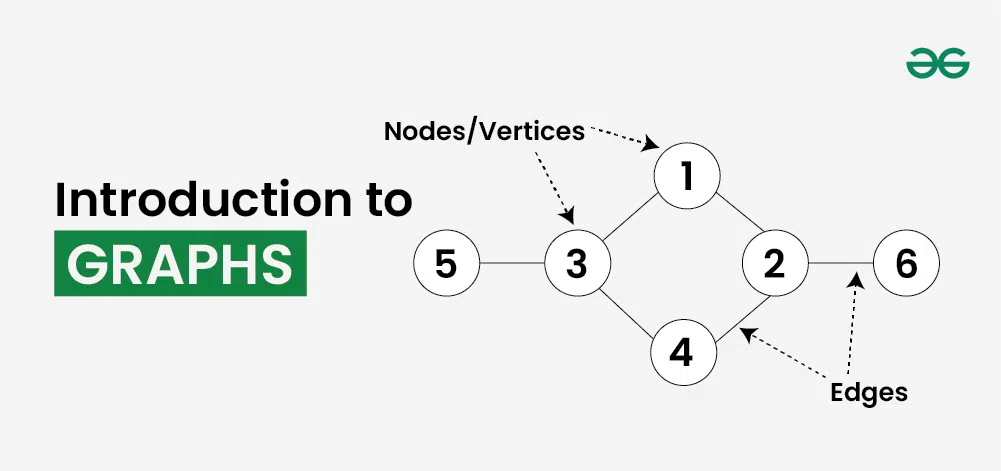102 Applications of BFS and DFS-1

A well-defined collection of distinct objects called elements or members. https://youtu.be/l56BfAgi5LA Learning Outcomes: To learn the applications of DFS and BFS To compare between DFS and BFS and to identify the connected components with BFS/ DFS

🧮

103 Applications of BFS and DFS-2

A well-defined collection of distinct objects called elements or members. https://youtu.be/yD4mk9nD_-s Exercise Questions

🧮

104 Breadth-first search

A well-defined collection of distinct objects called elements or members. https://youtu.be/WPaX9PFJY_4 Learning Outcomes: To explore reachability of a vertex in a graph- breadth first and depth first approaches

🧮

105 Complexity of BFS and DFS

A well-defined collection of distinct objects called elements or members. https://youtu.be/rCiV-4ceYRU Learning Outcomes: The students will be able to understand the complexity involved in BFS/DFS with respect to time and steps for finding the reachability.

🧮

106 Depth-first search

A well-defined collection of distinct objects called elements or members. https://youtu.be/1BvUzBkyD_o Learning Outcomes: To learn ‘depth first search’(DFS) algorithm and introduction to the concept of ‘stack’.

🧮

107 Directed Acyclic Graphs

A well-defined collection of distinct objects called elements or members. https://youtu.be/-VKVovlBnwE Learning Outcomes: The students will be able to understand the applications of directed acyclic graphs (DAGs) in daily life.

🧮

108 Introduction to Graphs

A well-defined collection of distinct objects called elements or members. https://youtu.be/wtQ6RtTwCVk Learning Outcomes: To explain the relation as a subset of the Cartesian product

🧮

109 Introduction to Graphs

A well-defined collection of distinct objects called elements or members. https://youtu.be/wtQ6RtTwCVk Learning Outcomes: To explain the relation as a subset of the Cartesian product

🧮

110 Representation of graphs

A well-defined collection of distinct objects called elements or members. https://youtu.be/4M-1F4DORps Learning Outcomes: To learn the concept of adjacency matrix; for directed and undirected graphs

🧮

111 Some general graph problems

A well-defined collection of distinct objects called elements or members. https://youtu.be/4K2wZkFKqIY Learning Outcomes: To learn the abstraction of the graph To learn the 4 color theorem, the concepts of covering the vertex, independent sets

🧮

112 Topological Sorting

A well-defined collection of distinct objects called elements or members. https://youtu.be/Rax3k-rCYkY Learning Outcomes: learn about topological sorting. find the possible sorting orders of DAGs.

🧮

113 Graded_Assignment_10

A well-defined collection of distinct objects called elements or members. https://youtu.be/wtQ6RtTwCVk Learning Outcomes: To explain the relation as a subset of the Cartesian product

🧮

114 All-Pairs Shortest Paths

A well-defined collection of distinct objects called elements or members. https://youtu.be/Rhm-0SD-NfE Learning Outcomes: The student will be able to: use Warshall’s algorithm as an alternative way to compute transitive closure..

🧮

115 Longest Paths in DAGs

A well-defined collection of distinct objects called elements or members. https://youtu.be/934a17SB5NY Learning Outcomes: The student will be able to: find the order of the dependencies using topological sorting.

🧮

116 Longest Paths in DAGs

🧮

117 Matrix Multiplication

A well-defined collection of distinct objects called elements or members. https://youtu.be/N_PvNrQXUg4 Learning Outcomes: Understand the operation of matrix multiplication and its use in finding reachability.

🧮

118 Minimum Cost Spanning Tress

A well-defined collection of distinct objects called elements or members. https://youtu.be/3GwJAstzzBk Learning Outcomes: The student will be able to understand the concept of spanning tree, minimum cost spanning tree and its characteristics .

🧮

119 Minimum Cost Spanning Tress - Kruskal's Algorithm

A well-defined collection of distinct objects called elements or members. https://youtu.be/-0diRWTGgk8 Learning Outcomes: The student will be able to compute minimum cost spanning trees using Kruskal’s algorithm and the concept of correctness of Kruskal’s algorithm.

🧮

120 Minimum Cost Spanning Tress - Prim's Algorithm

A well-defined collection of distinct objects called elements or members. https://youtu.be/btr8zJBgaQg Learning Outcomes: The student will be able to compute minimum cost spanning trees using Prim’s algorithm and the concept of correctness of Prim’s algorithm.

🧮

121 Shortest Paths in Weighted Graphs

A well-defined collection of distinct objects called elements or members. https://youtu.be/4l_g6IQz6Go Learning Outcomes: The student will be able to: the shortest path problems such as single source shortest paths and all pair shortest paths.

🧮

122 Single Source Shortest Paths

A well-defined collection of distinct objects called elements or members. https://youtu.be/XXFcZyP2KlM Learning Outcomes: The students will be able to understand the conceptual numerical on single source shortest paths and Dijkstra’s algorithm.

🧮

123 Single Source Shortest Paths with Negative Weights

A well-defined collection of distinct objects called elements or members. https://youtu.be/FGGMybRD4O4 Learning Outcomes: The students will be able to understand the conceptual numerical on single source shortest paths with negative weights using the Bellman-Ford algorithm.

🧮

124 Transitive Closure

A well-defined collection of distinct objects called elements or members. https://youtu.be/6Ax9K7gSuJE Learning Outcomes: Understand the representation of relationships using graphs. Understand the concept of transitive closure and finding the reachability.

🧮

125 Graded_Assignment_11

🧐

126 Revision lecture on Set Theory

A well-defined collection of distinct objects called elements or members. https://youtu.be/n514TARtjyA